SUMMARY
In the Czech Republic, hydrogeological zones were defined as early as 1965 as a part of the regional hydrogeological survey. A hydrogeological zone (HGZ) is defined as a unit with similar hydrogeological conditions, defined tectonically and geologically, in whose territory a certain type of aquifer and groundwater circulation prevails. The boundaries of HGZs have been modified over time and their numerical hydrogeological characteristics have been determined by various methods; one of the basic characteristics is the amount of natural groundwater resources. Natural resources are the dynamic component of groundwater and are expressed in m3.s-1. They are determined by the recharge of water to the aquifer system (precipitation, groundwater overflows from other aquifers, natural infiltration of surface water, etc.). If the HGZ is hydrogeologically closed, the long-term average of its recharge from precipitation and the long-term average of baseflow can be used as an estimate of the natural groundwater resource. In the “Groundwater Rebalance Project”, estimates of natural groundwater resources in 152 hydrogeological zones in the Czech Republic were processed and are presented in the report [1]. The natural resources were determined by several different methods using data from 1971–2010 and 2000–2010.
Due to the intensive increase in average annual air temperatures in the Czech Republic after 1980, and with special consideration of the dry period 2014–2019, we used data from the period 1981–2019 for the current estimation of natural groundwater resources in the hydrogeological zones. The applied method of calculation was based on determination of total runoff from the hydrogeological zone and its conversion to baseflow using the baseflow index (BFI), the regional elaboration of which is included in the study [2]. Two calculation alternatives were used to determine total runoff: by the balance difference between precipitation and estimated evapotranspiration and by the regression relationship between precipitation and runoff. Both types of relationships were derived from the results of flow monitoring at Czech Hydrometeorological Institute (CHMI) water gauging stations and from monitoring of rain gauge and climate stations. For each HGZ, a relationship derived from data of the basins in which the zone lies and which it is adjacent to was used, taking into account the orographic similarity of the zone and the basin. Long-term averages of precipitation and temperature were calculated for the HGZ. According to these relationships, long-term total runoff averages were determined by interpolation or extrapolation.
The results of the calculations showed that the method based on regression of runoff on precipitation gives estimates on average 5 to 6% greater than the method using evaporation estimates. Both calculation alternatives, when compared to previous results from the “Groundwater Rebalance Project”, show a decrease in average baseflow, and a corresponding decrease in average groundwater recharge, of approximately 7 to 12% during the 1981–2019 period compared to the 1971–2010 period. The decrease can be attributed to an increase in average air temperature of approximately 0.4 °C between the compared periods, with nearly unchanged average precipitation. The observed changes in natural groundwater resources over the two periods show regional differences due to the hydrogeological characteristics not included. As the results were not obtained by the same methods, their use for intercomparison is limited. The results for the HGZ show changes in the interval ± 20% for 61% and 72% of the cases, respectively, depending on the method used.
INTRODUCTION
Determining the usable amount of groundwater for sampling is one of the basic tasks of hydrogeological research. The main part of this work is the assessment of the size of groundwater resources within the defined balance hydrogeological unit. For these purposes, hydrogeological zones (HGZ) were defined as basic balance units used to determine the size of groundwater resources. The Czech Republic is divided into 152 HGZ.
The size of groundwater resources is determined spatially (in the optimal case, it refers to a hydrogeological structure with a closed groundwater cycle, which contains both infiltration and drainage areas) and temporally (both in terms of a time interval, e.g. a hydrological year, and in terms of temporal variability formation of groundwater resources due to temporal fluctuations of hydrological parameters).
Three types of groundwater resources are distinguished: natural, induced, and artificial. Natural resources are formed under natural, mostly unaffected conditions in a certain hydrogeological unit in a defined period of time. Under anthropogenically changed conditions, induced resources (e.g., bank infiltration near abstraction facilities) and artificial resources (e.g., artificial seepage of water into underground structures) may arise.
This article refers to natural groundwater resources in individual HGZ which are formed in the area of these zones. Hydrological balance approaches were used, which are based on the fact that infiltrated precipitation is the main source of groundwater formation. Natural groundwater resources as a dynamic component of their reserves are determined by the process of hydrological balancing as spatio-temporally defined baseflow. It is necessary to see the limits of the hydrological methods used, which in principle cannot include overflows between collectors, as well as induced groundwater resources, which manifest themselves, for example, in Quaternary zones (the influence of bank infiltration, or ongoing drainage from subsoil units, etc.).
The size of natural groundwater resources can be estimated using a combination of different methods, which can be divided into three basic groups: first, according to the amount of infiltration; second, according to the underground flow through the corresponding collector; and third, according to the amount of water that is drained from this system.
The dry period of 2014–2019 had a significant impact on the size of groundwater resources, as evidenced by the lowering of groundwater levels within groundwater monitoring in the CHMI nationwide network. In the “Groundwater Rebalance Project” (2011–2016), estimates of natural groundwater resources were made in all 152 HGZs based on input hydrological data for the period 1971–2010, with comparative use of partial data for the period 2000–2010. The determination therefore did not include the following dry season. At present, it has already been possible to proceed with a new balance estimate based on data from the period 1981–2019 and try to compare the results with the previous outputs of the “Groundwater Rebalance Project”.
However, a direct comparison of the achieved results for both periods is hindered by the different methodological approaches that were chosen to determine natural resources in individual HGZs in the “Groundwater Rebalance Project”. This was related to the different level and amount of available data that had to be reckoned with in different zones. As follows from the report [3], a more detailed approach was chosen in 55 defined zones, where measured data was also used. Derived regression relationships between precipitation and runoff and between precipitation and baseflow, or a balance approach using a balance equation including determination of evaporation, were chosen to determine natural resources. The final list of natural resources were the result of an individual assessment of the results achieved using different methods according to the specific situation of each zone.
In another 30 HGZs, detailed hydrological balance models were processed and their outputs used to determine the baseflow. In another seven HGZs, it was not possible to determine natural groundwater resources, mainly due to the massive anthropogenic impact of the areas, mostly through the extraction of raw materials. That left 60 zones where the base runoff was estimated using the chosen hydrological approaches. In 31 zones created by division of the original zones, the method of analogues and the distribution of precipitation within the zones was used to determine baseflow, and for the remaining 29 zones, original values from 2006 were used, converted to averages and to the period 1981–2010. The procedures used are described in detail in the report [1].
As shown below, the new results obtained on the basis of the derived balance and regression relationships are thus not completely comparable with the older data in order to mechanically compare the numbers for the two periods. Their comparison can only be done individually within individual zones.
METHODOLOGY
One of the basic methods of determining the groundwater recharge is the use of a hydrological balance model which allows the calculation of the time course of groundwater recharge. Normally, the parameters of the model are calibrated according to data from the catchment area of water gauging stations so that runoff modelled according to precipitation and air temperatures is as close as possible to observed runoff. Except for cases where the HGZ coincides with the catchment area of the water gauging station, the estimate of runoff from the HGZ is based on the results of modelling of the catchments into which the HGZ extends to, and from nearby catchments with a similar hydrogeological character. In this procedure, the parameters and input variables – precipitation and air temperature – evaluated for the HGZ area are transferred to the hydrological balance model. The described procedure is quite complex and laborious, usually requiring the calculation of several solution variants, their assessment, and selection of the resulting estimate.
If the purpose of groundwater recharge estimate is not its time course, but only the long-term annual average, instead of transferring the model solution, information can be used from the balance relationships from the basins in which the HGZ is located, as well as neighbouring basins. The calculation is based on determination of total runoff from the HGZ and its conversion to baseflow using the baseflow index (BFI). To determine total runoff, two calculation alternatives were used: first, according to the balance difference between precipitation and estimated areal evaporation, and second, according to the regression relationship between precipitation and runoff.
DERIVATION OF RELATIONSHIPS FOR ESTIMATING AVERAGE ANNUAL RUNOFF
Calculation of runoff as the difference in precipitation and areal evaporation
The calculation of the long-term averages of groundwater recharge in HGZ uses the basic relationships of hydrological balance, according to which the long-term average of total runoff R [mm.year-1] is the difference between the long-term average of precipitation P [mm. year -1] and the long-term average of areal evaporation E [mm. year -1]. In the balance equation of long-term averages from several decades, if we ignore change in water supplies, the following applies:

This equation (1) can be applied to the hydrological catchments of water gauging stations on the assumption that the catchment is not only morphologically, but also hydrogeologically closed, i.e. there are no inflows or outflows of water between neighbouring catchments. Areal evaporation can then be estimated as the difference between observed precipitation and runoff calculated from the monitored flows. If the difference P – R deviates from the regional level, an increase indicates runoff outside the closing profile, and a decrease indicates inflow of groundwater from the neighbouring catchment or collector.
The variable that is considered to be the upper limit of areal evaporation is the potential evapotranspiration (PET). To calculate it, we used the following equation:
PET = 37.9 . T + 289.4 (2)
where
PET is average annual potential evapotranspiration [mm.year-1]
T average annual air temperature [°C]
Equation (2) when applying the areal evaporation calculation method according to Oudin [4], was recommended for the Czech Republic by Beran et al. in their study [5].
According to this equation, potential evapotranspiration increases linearly with increasing air temperature. Since the relationship between air temperature and precipitation is mostly linear, a decrease in potential evapotranspiration with increasing precipitation is usually linear. This can be seen in Fig. 1, which shows the courses of the balance variables depending on precipitation. The course of areal evaporation plotted against precipitation is non-linear and shows that, in the interval of precipitation less than about 600 mm (where precipitation is less than potential evapotranspiration), evaporation increases with precipitation and is limited by precipitation. Above the specified limit for increasing precipitation, evaporation decreases; the influence of the decrease in potential evapotranspiration corresponding to the decrease in air temperature prevails. The change described is continuous and is manifested by the curvature of the relationship between precipitation and runoff.
The courses shown in Fig. 1 serve as an example. The data come from a set of catchments of water gauging stations from the Svratka basin above the Svitava tributary. The results from other basins have a similar course; the area of change in areal evaporation trend is mostly in the interval of average annual precipitation of 600 to 700 mm.
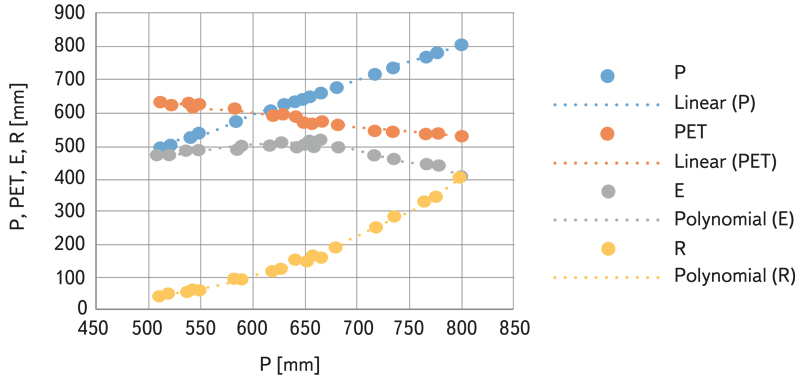
Fig. 1. Long-term annual averages of balance variables plotted against average annual precipitation; an example derived from observed data from water gauging stations in the Svratka basin above the Svitava tributary
A procedure was developed for regional analyses in which relative variables are used from the point of view of the influence of air temperature, or potential evapotranspiration. Evaporation is characterized by the E/PET ratio, so we estimate it as a percentage of potential evapotranspiration. The variability of the E/PET ratio, depending on precipitation, corresponds to the above-described cumulative effect of precipitation and temperature on the amount of areal evaporation. The E/PET ratio increases with increasing precipitation up to the area where there is sufficient temperature for evaporation, and then it decreases for the fact that falling air temperature limits evaporation. The P/PET ratio can be used as an independent variable; see [6]. An example of such processing is shown in Fig. 2. We used this type of correlation analysis to estimate average evaporation and, based on this, calculated an estimate of average annual runoff by subtracting it from precipitation. For the analytical expression of the correlation relationship between P/PET and E/PET, we used a second degree polynomial in most catchment areas.
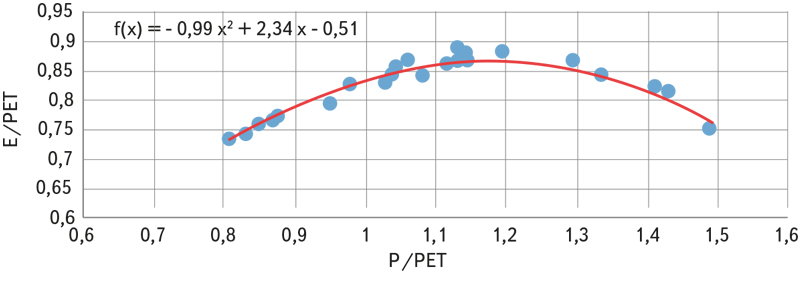
Fig. 2. Example of the relationship between E/PET ratio and P/PET ratio, observed data from water gauging stations in the Svratka basin above the Svitava tributary
Regression relationship of runoff and precipitation
To express the relationship between long-term average annual precipitation P [mm] and average long-term runoff R [mm], a non-linear dependence – a second degree polynomial, see Fig. 1 – proved suitable.

The parameters a, b, c of relationship (3) describe the shape of the function R = f(P) corresponding to the fact that areal evaporation reaches its maximum in the area where the combination of precipitation and temperature is optimal for it. The non-linear courses of runoff dependence on precipitation are clearly visible when analysing data with a large range of precipitation. When analysing local data with a smaller precipitation range, linear function also provides usable results.
Data selection procedure for deriving a relationship for estimating average annual runoff for individual hydrogeological zones
With a few exceptions, both procedures described above were used for all HGZs.
We derived parameters of the relationships from the flow monitoring results in CHMI water gauging stations and according to monitoring of rain gauging stations and climate stations in the basins and their surroundings. Monthly series were processed; average monthly flows were supplemented with water use and reservoir operation. From the monthly series, long-term annual averages of runoff, precipitation, and temperatures were calculated in the catchment area of the water gauging stations. Data from 1981–2019 were used, providing that there is an evaluated flow monitoring for at least 18 years in a row. During processing, isolated cases were excluded in which the relationship of precipitation and air temperature or the relationship of precipitation and runoff quite obviously deviated from the range of data in neighbouring basins. After this reduction, the used set contained data for the basins of 395 water gauging stations.
The selection of stations for deriving relationships was also influenced by what data and how reliable it was for the area around a specific HGZ and its surroundings. For several HGZs, we could not find data to use the relationship between the E/PET ratio and P/PET ratio, so the result is only runoff estimates based on the precipitation-runoff relationship.
For individual hydrogeological zones, the selection of water gauging station basins from which both types of relationships described above were derived was directed, on the one hand, by an effort to capture regional differences in the hydrological and hydrogeological regime, and on the other hand, by the need for at least a minimum number of cases that allow to estimate the correlation relationship.
Special attention had to be paid to the few cases with very small precipitation in the HGZ, less than the minimum precipitation in the catchment data set used to derive the relationship. The derived analytical relationship was then used for extrapolation, and other types of relationship than the standard polynomial of the second degree had to be considered.
During the calculations, estimates of total runoff determined by both described procedures were continuously compared. In some cases, significantly deviating results were identified and the probable cause of the deviation was sought. Relationships between precipitation and air temperatures were also used here, according to which estimation of precipitation for several small basins showed to be inaccurate. On rare occasions, data from deviating results were excluded from deriving the relationships.
For the deduction of long-term averages of groundwater recharge in a hydrogeological zone, we assume that the balance relationship, derived on observed basins in the area where the HGZ is located, describes the balance in the zone with an acceptable degree of agreement.
We obtained an estimate of the total average annual runoff from the HGZ by substituting average annual precipitation and average annual air temperatures, calculated from observations of rain gauge and climate stations in the HGZ, into the relationships compiled for the area in which the HGZ lies.
CONVERSION OF AVERAGE ANNUAL RUNOFF FOR INDIVIDUAL HYDROGEOLOGICAL ZONES TO AVERAGE ANNUAL GROUNDWATER OUTFLOW
From the estimation of runoff R for each hydrogeological zone according to the equation

The long-term average of the baseflow Rz was calculated, which in a long-term average, neglecting changes in water reserves, corresponds to the average groundwater recharge from precipitation. It does not include possible water overflows between HGZs. The values of the BFI (baseflow index, i.e. the ratio between baseflow and total runoff) were taken from an article [2]. For several HGZs, they were derived from an observed series of average daily flows at a water gauging station whose catchment lies in the relevant HGZ, or has similar hydrogeological characteristics. The determination procedure is described in the cited article.
CALCULATION RESULTS
To show the results, average annual runoff from the HGZ were recalculated to average specific groundwater outflows from the HGZ [l.s-1.km-2]. These values are recorded in Fig. 3–8, broken down by type of hydrogeological structures. For the calculation based on estimation of runoff as the difference of precipitation and evaporation, they are shown in the map in Fig. 9. Due to overlaps, the areas of the Quaternary HGZ are not plotted on it.
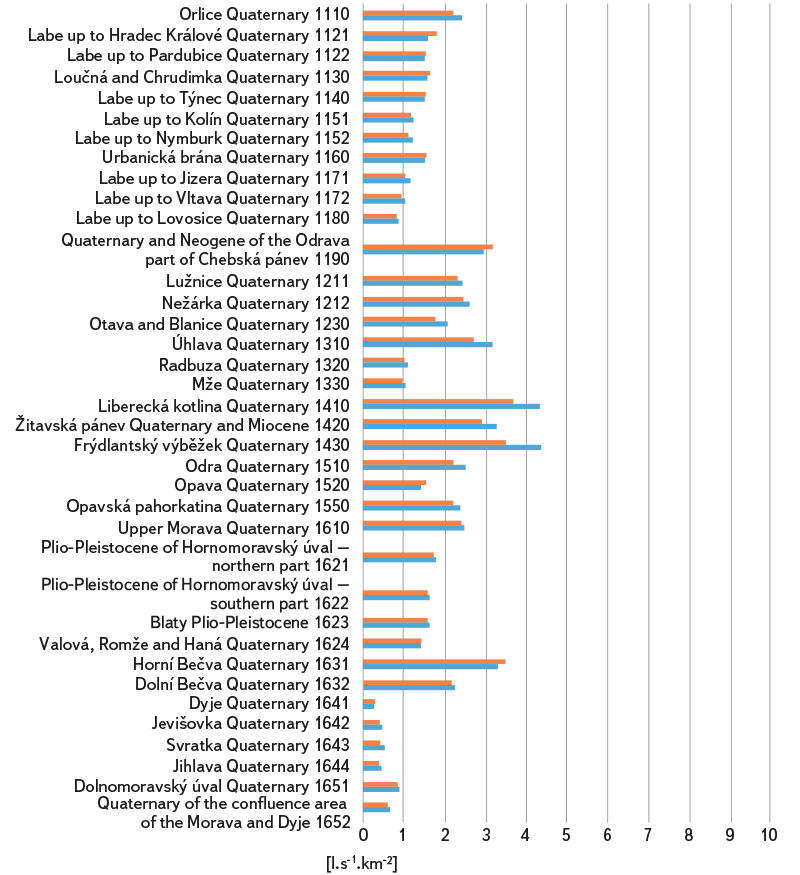
Fig. 3. Specific groundwater outflows from hydrogeological zones – Quaternary formations; estimates based on precipitation-runoff relationship are shown in blue, and estimates based on runoff as the difference between precipitation and evaporation are shown in red
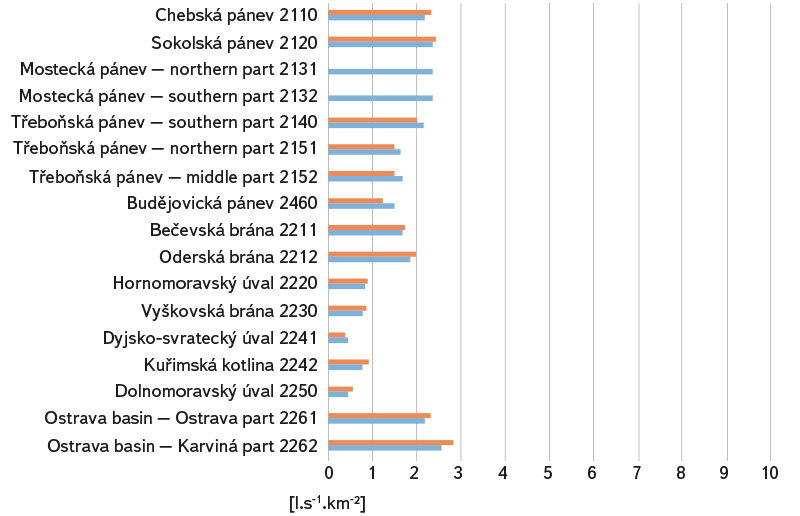
Fig. 4. Specific groundwater outflows from hydrogeological zones – Tertiary and Cretaceous basin formations; estimates based on precipitation-runoff relationship are shown in blue, and estimates based on runoff as the difference between precipitation and evaporation are shown in red
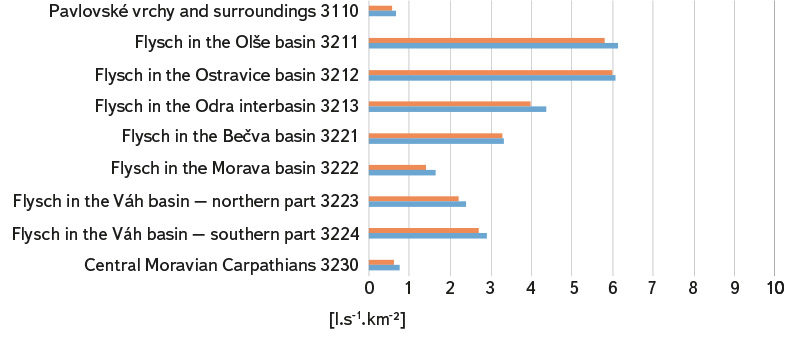
Fig. 5. Specific groundwater outflows from hydrogeological zones – Flysch sediments; estimates based on precipitation-runoff relationship are shown in blue, estimates based the runoff as the difference between precipitation and evaporation are shown in red
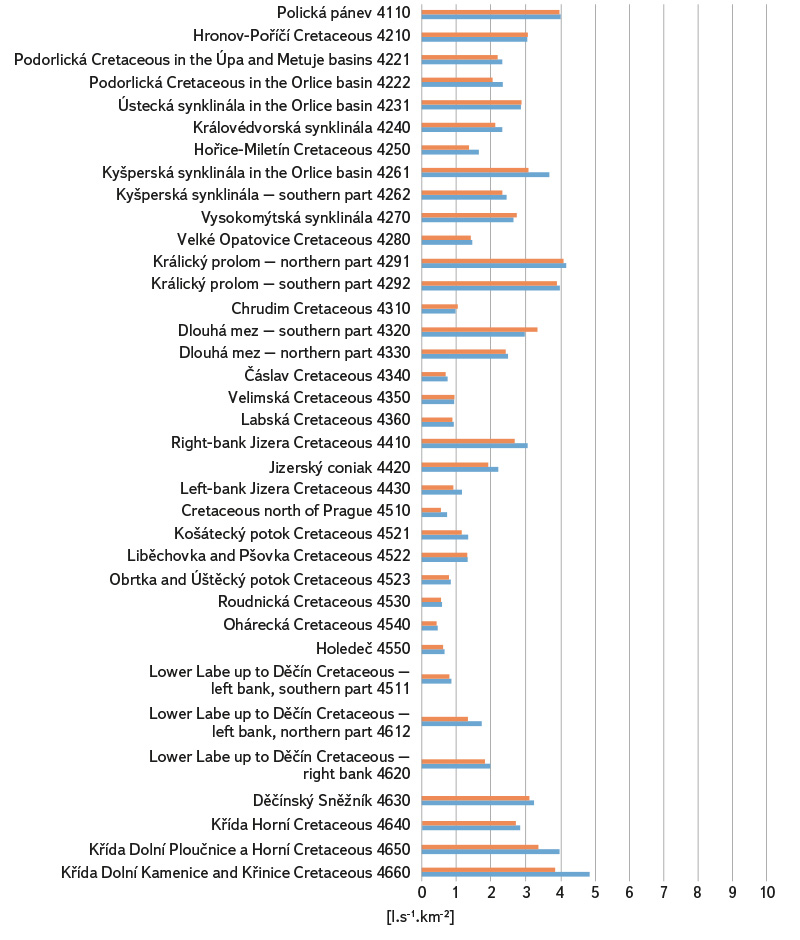
Fig. 6. Specific groundwater outflows from hydrogeological zones – Upper Cretaceous sediments; estimates based on precipitation-runoff relationship are shown in blue, and estimates based on runoff as the difference between precipitation and evaporation are shown in red
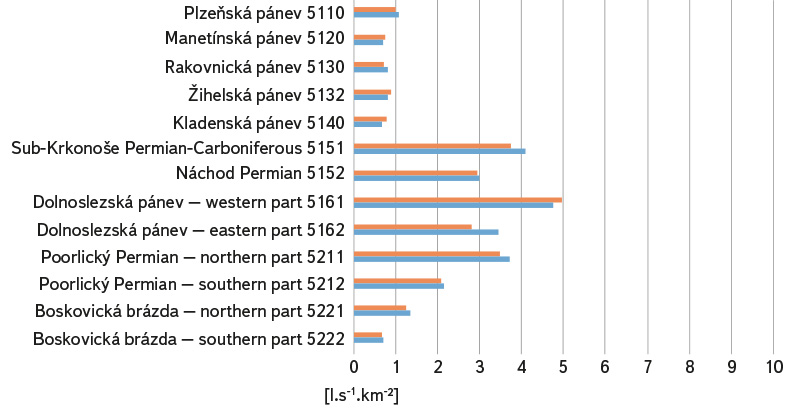
Fig. 7. Specific groundwater outflows from hydrogeological zones – Permocarbon limnic basins and trenches; estimates based on precipitation-runoff relationship are shown in blue, and estimates based on runoff as the difference between precipitation and evaporation are shown in red
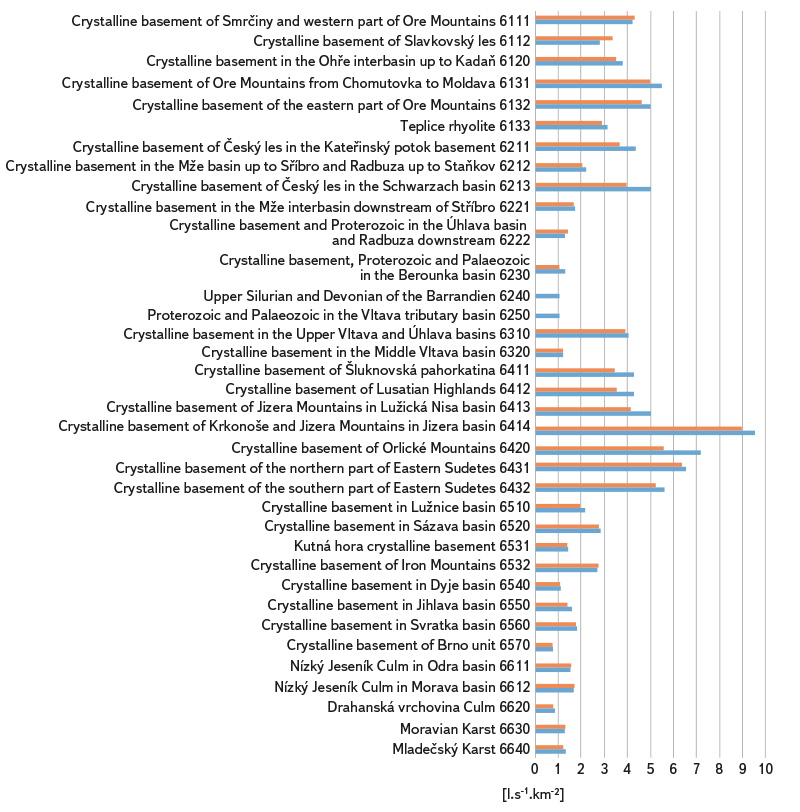
Fig. 8. Specific groundwater outflows from hydrogeological zones in a hydrogeological massif; estimates based on precipitation-runoff relationship are shown in blue, and estimates based on runoff as the difference between precipitation and evaporation are shown in red
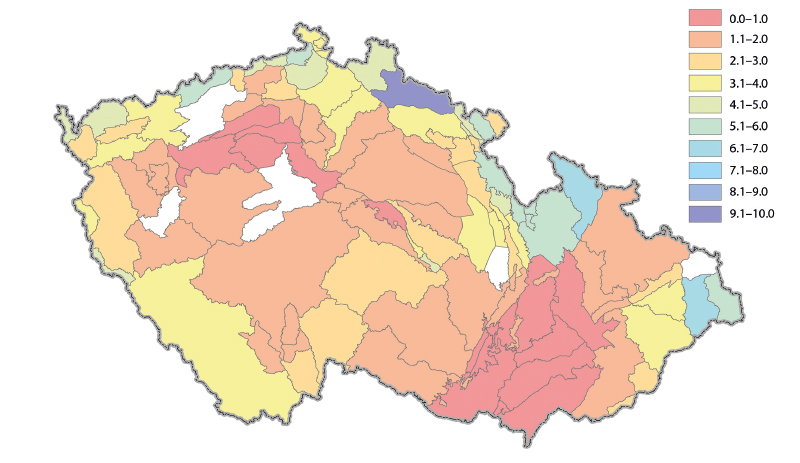
Fig. 9. Estimates of specific groundwater baseflow determined from runoff estimates (difference between precipitation and evaporation) in [l/s/km2]; no results for uncoloured zones from previous overall assessment.
COMPARISON OF RESULTS ACCORDING TO ESTIMATION PROCEDURES
Tab. 1 compares the characteristics calculated from the entire set of processed HGZs. It is clear that the procedure based on regression estimate of runoff according to precipitation amount provides estimates on average 5 to 6% larger than the method using evaporation estimate. Deviations in individual HGZ are in the range of 19.8 to 22.8%. The difference in the results of used procedures probably corresponds to the fact that the parameters of the relationships are estimated in alternative procedures according to the agreement of different variables. In addition, average air temperature is used in the procedure based on estimation of areal evaporation, which can also influence the resulting values.
Tab. 1. Comparison of calculated characteristics for the whole set of processed zones

COMPARISON OF RESULTS WITH ESTIMATES FROM THE “GROUNDWATER REBALANCE PROJECT”
As part of the “Groundwater Rebalance Project”, estimates of natural groundwater resources in 152 hydrogeological zones in the Czech Republic were prepared, which are presented in the report [1]. Natural resources were determined by several different procedures using data from the period 1971–2010 and 2000–2010.
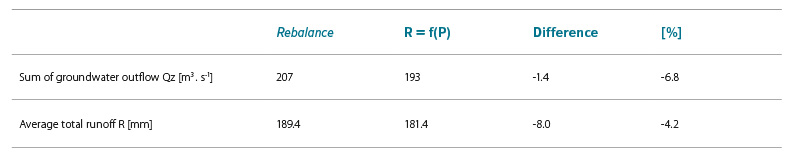
The comparison of the summary results of the performed calculations with the corresponding values from the previous processing in Tab. 2–4 shows that although in the newly used period 1981–2019 atmospheric precipitation in the HGZ was less than 1.6% on average, groundwater outflow decreased by an average of 6.8% according to the calculations of precipitation-runoff relationships, and by 11.9% according to relationships based on areal evaporation estimate. Decreases in average total runoff R of 8–19.6 mm agree reasonably well with the result of an article [7], in which the relationship between a warming of 1 °C and a decrease in the runoff in the range of 15–45 mm is presented. This corresponds to a range of 6–18 mm for a warming of 0.4 °C. Warming of 0.4 °C occurred in the Labe up to Děčín and the Dyje up to Dolní Věstonice basins; it was smaller in the Upper Morava basin and in the Odra basin.
The map in Fig. 10 shows the areas in which application of the estimate of natural groundwater resources by the procedure based on calculation of average runoff from the basin according to the difference in precipitation and evaporation leads to values greater, or smaller than the corresponding data from the previous processing mentioned above.
Tab. 2. Overall differences between data from the “Groundwater Rebalance Project” and data from the regression relationship R = f(P)
Tab. 3. Overall differences between data from “Groundwater Rebalance Project” and data from the R = P – E balance relationship

Tab. 4. Differences in long-term averages of precipitation and temperature between the two assessed periods 1971–2010 and 1981–2019
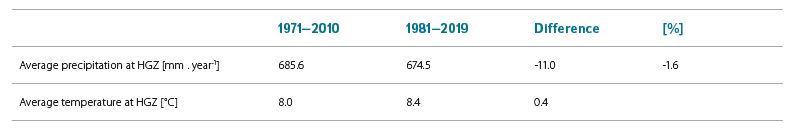
Both calculation alternatives, when compared with previous results from the “Groundwater Rebalance Project”, show, according to long-term averages, a decrease in average baseflow, and thus also in average groundwater recharge in 1981–2019 compared to 1971–2010 in the range of about 7–12%, which can be attributed to an increase in average temperature by about 0.4 °C (with almost unchanged average precipitation). In area vies, areas with decrease predominate. When using the results, it should be taken into account that the compared values were not obtained using the same methodological procedure and estimates for individual HGZ are also burdened by uncertainty when determining input variables.
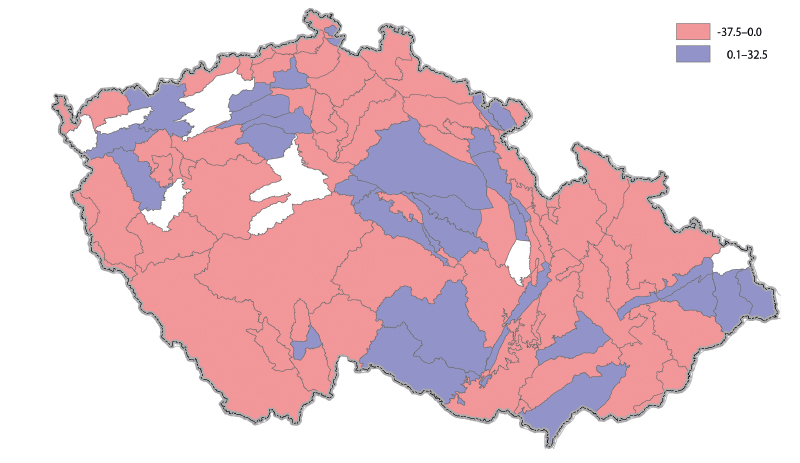
Fig. 10. Differences in the estimate of specific groundwater baseflow determined from the estimate of runoff as a difference in precipitation and evaporation from the results of the previous overall assessment, expressed as a percentage; no results for uncoloured zones from the previous overall assessment
CONCLUSION
The described procedure estimates natural resources of HGZ corresponding to recharge of the runoff regime from precipitation; it does not include recharge from watercourses in Quaternary zones or possible overflows of groundwater between zones and collectors. The estimate is based on determination of total runoff from the HGR and its conversion to basic outflow using the BFI. To determine total runoff, two calculation alternatives were used: first, according to the regression relationship between precipitation and runoff; and second, according to the balance difference between precipitation and estimated areal evaporation. A procedure based on regression estimation of runoff according to precipitation provides estimates that are on average 5–6% larger than a procedure using evaporation estimation.
When compared with previous results from the “Groundwater Rebalance Project”, according to long-term averages, both calculation alternatives show a decrease in average baseflow, and thus also in the groundwater recharge in 1981–2019 compared to 1971–2010 in the range of about 7–12%, which can be attributed to an increase in average temperature by about 0.4 °C (with almost unchanged average precipitation). Changes in natural groundwater resources show regional differences. Given that the results used for comparison were not obtained using the same methods, the changes for individual HGZs range within ± 20%, namely for 61% and 72% of the cases, respectively.
Acknowledgements
The article was written as part of the PERUN project, activity 1.3 – Assessment of the status and development of natural groundwater resources. The project is financed by the Technology Agency of the Czech Republic.
This article has been peer-reviewed.
The article was translated on the basis of the Czech original by Environmental Translation Ltd.
