ABSTRAKT
Klimatická změna se projevuje na řadě míst výrazně prostorově lokalizovanými přívalovými srážkami s krátkou dobou svého trvání, zato však s velkou intenzitou. Jako jeden z očekávaných důsledků takovéhoto typu srážek je i vznik bleskových povodní, vyznačujících se prudkým vzestupem z hodnoty běžného průtoku na hodnotu kulminačního průtoku a opětovného rychlého poklesu. Důsledkem výskytu tohoto typu epizodálních povodňových jevů je iniciace morfologických přeměn v korytech menších a středních podhorských vodních toků, často až s devastačními účinky pro úsek koryta vodního toku. Článek shrnuje výzkum vzniku a vývoje výmolu v úseku toku na přechodu od opevněného koryta s tvarově fixovanými břehy a dnem ke korytu, které může být zcela nekontrolovaně morfologicky přetvářeno. Hlavní pozornost byla v rámci tohoto výzkumu věnována formulaci parametrického modelu morfologického vývoje výmolu na přechodu mezi opevněným a neopevněným (rozvolněným) korytem. Poznatky z tohoto modelu mohou být využity jak pro pochopení hydraulicko-morfologických procesů, jež vznikají v místě náhlé přeměny koryta, tak i pro praktický návrh revitalizačních úprav koryta na přechodu od plně opevněného koryta ke zcela rozvolněnému korytu.
ÚVOD
Revitalizační úpravy koryt vodních toků představují jedno z adaptačních opatření v oblasti snižování dopadu sucha na vodní režim krajiny. Tato adaptační opatření patří mezi nosná témata výzkumné činnosti projektu SS02030027 „Vodní systémy a vodní hospodářství v ČR v podmínkách změny klimatu (Centrum Voda)“. Jde zejména o oblast návrhu opatření vedoucích ke snížení povodňových rizik se zaměřením na aspekty ovlivnění průběhu povodní změnou klimatu. Rovněž sem spadá výzkum dopadu klimatické změny na ekosystémy a snížení důsledků antropogenního ovlivnění vodního a na vodu vázaného prostředí a vytváření podmínek pro zlepšení ochrany ekosystémů. Revitalizace koryta vodního toku je dnes v užším hydromorfologickém měřítku vnímána jako soubor opatření, jež umožňují utváření koryta za přítomnosti širokého spektra korytotvorných, především fluviálních procesů. K těmto procesům v korytech vodních toků patří i vytváření hydraulických proudových struktur – např. kontrakce a expanze proudu, vznik úplavů s přítomností vírů s vertikální osou a vznik vodního válce s vodorovnou osou jako součást vodního skoku. Dále pak vznikají erozní, transportní a sedimentační procesy, které jsou navázány na předchozí hydraulické jevy. Závisí na geomechanických vlastnostech materiálu, v němž se koryto přetváří, a na stabilitě břehů, které se svou deformací výrazně podílejí na proměnlivé geometrii koryta. Při návrhu revitalizačních úprav je vhodné vycházet právě z poznatků a pozorování sukcesních procesů podílejících se na přetváření koryta. Výrazné morfologické změny lze pozorovat v terénních podmínkách během průchodů bleskových povodní i po nich, kdy morfologické změny mají značně akcelerovaný průběh. Dále lze morfologické změny pozorovat při cíleném fyzikálním výzkumu v laboratorních podmínkách, v nichž lze detailněji sledovat a vyhodnotit průběh procesu, který by však měl být pokud možno verifikován pro podmínky, jež jsou co nejbližší reálným korytům. V tomto příspěvku se autor věnuje vzniku a vývoji prostorového výmolu, pro svůj charakteristický tvar často nazývaného „výmol – hruška“, který vzniká na přechodu mezi opevněným a neopevněným korytem. To dobře odpovídá i revitalizačním úpravám vodních toků, v minulosti poznamenaných soustavnými melioracemi, při nichž docházelo k odstraňování opevnění v celých úsecích koryta.
Výzkum výmolu v přechodové oblasti rozvolněného koryta
Problematikou stabilizace rozvolněného koryta v jeho rozšíření se již dříve zabývala řada autorů, namátkou [3, 7]. Výzkum VÚVH Bratislava [3], který se svým charakterem asi nejvíce blížil této studii prostorového výmolu, přijal jako první pro tento morfologický objekt na vodním toku pracovní označení „hruška“ (obr. 1 vpravo). Ačkoli byl výzkum proveden na modelu objektu typu „hruška“ v několika tvarových alternativách, a to i s uvážením vlivu transportu splavenin z horních částí vodního toku, nebyly uvedeny kromě obecných doporučení pro konstrukci těchto objektů metody jejich hydrotechnického řešení.
Vlastní výzkumný projekt autora, zabývající se morfologickými změnami na malých, relativně strmých podhorských vodních tocích za vysokých průtoků, byl prováděn ve dvou etapách:
Terénní šetření s pozorováním reakce koryt na přirozené nebo uměle vyvolané morfologické změny. Cílem této etapy bylo provést kvalitativní popis změn.
Laboratorní modelové experimenty, které byly zaměřeny na návrh kvantitativního modelu morfologických přeměn se schopností předpovídat morfologickou odezvu koryta při použití ekologicky šetrných a nákladově efektivních revitalizačních opatření.

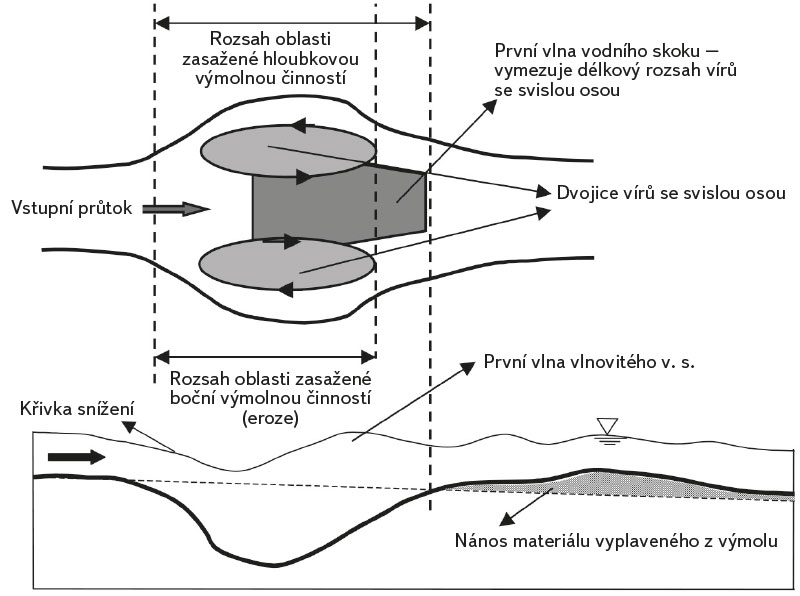
Obr. 1. Vývoj „výmolu – hrušky“ iniciovaného porušením spádového stupně při povodni (vlevo); schematické naznačení charakteru proudění v přechodové oblasti prostorového výmolu (vpravo)
Fig. 1. Development of the “pear shaped” scour resulting from degradation of a drop structure on flash flood occurrence (left); feature of flow in transitional zone of the spatial 3D scour (right)
V části projektu, jehož cílem bylo umožnit kvantifikaci morfologických změn, probíhal soustavný výzkum v laboratorních podmínkách na dvou odlišných typech modelu koryta v přechodové oblasti. Pro komplexnější popis chování modelu byla zvolena „úplná prostorová“ realizace koryta v přechodové oblasti jeho rozvolnění (obr. 2 vlevo). Pro urychlení postupu dokumentace okamžitého vývoje výmolové prohlubně koryta byla navržena realizace symetricky zjednodušeného „polovičního“ koryta (obr. 2 vpravo). Osou symetrie koryta zde byla skleněná stěna hydraulického žlabu, v němž bylo koryto ve vstupní opevněné části i přechodové rozvolněné části vytvořeno. Tato druhá realizace umožňovala velmi rychle zachytit průběh hladiny a dna v podélném směru prakticky v daném okamžiku. Pro urychlení geometrického zaměření hladiny i dna byla využita optická přístupnost přes skleněnou boční stěnu žlabu. Taktéž proměření rychlostních polí v přechodové oblasti koryta bylo možno provést výrazně rychleji než při úplné prostorové realizaci koryta. Je zřejmé, že předpoklad symetrie byl i z hlediska reálného vývoje koryta v rozvolnění zjednodušujícím předpokladem, který bylo nutno v další fázi projektu verifikovat s úplnou prostorovou realizací modelu koryta. V zásadě by neměly být žádné objektivní důvody pro výrazně nesymetrický vývoj výmolu, pokud k tomu ovšem nejsou vytvořeny zvláštní podmínky. Další podrobnosti o výzkumu jsou popsány v literatuře [5, 6] a pro stručnost zde nejsou uvedeny.

Obr. 2. Úplný prostorový model koryta v přechodové oblasti vývoje výmolu (vlevo); poloviční model koryta s osou symetrie ve skleněné stěně žlabu (vpravo) – vše v laboratorních podmínkách
Fig. 2. Full space model of the channel in the transition zone of scour hole development (left); symmetric half-space model of the channel with axis at the flume glass wall (right) – all under laboratory conditions
Pozorovaný vývoj výmolu v úplném modelu koryta
Na základě pozorování sukcesního vývoje prostorové prohlubně výmolu v nekohezních materiálech lze shrnout dílčí poznatky (viz schéma na obr. 1 vpravo):
Na přechodu mezi pevným a deformovatelným korytem začíná celý proces vznikem malé prohlubně ve dně tak, jak k tomu dochází i u širokých koryt. Při samovolném utváření prahu ve dně na přechodu mezi koryty vzniká proudění charakteru vodního skoku. Nejdříve jde o proudění s povrchovým válcem nebo o vlnovitý vodní skok.
S rostoucí hloubkou prohlubně nemění toto proudění v podélné rovině výrazně svůj charakter. Jakmile prohlubeň dosáhne pat svahů, dojde k poruše jejich stability a malé části nebo i celé bloky materiálu začnou sjíždět do prohlubně. Svahy přetvárného koryta v blízkosti své paty již plynule nenavazují na svahy pevného koryta. Dochází zde k odtrhávání proudu od stěny a vznikají první boční víry u pat obou svahů.
Boční víry začínají postupně narůstat a sílit. Hlavní část své cirkulační energie dostávají od hlavního proudu v blízkosti osy koryta. Boční válce se z obou stran rozpínají, stlačují středový proud a vedou k jeho šířkové kontrakci. Znásobuje se tím tečný účinek proudu u dna a od tohoto okamžiku postupuje prohlubování výmolu velmi rychle.
Čím více se výmolová prohlubeň rozšiřuje do stran, tím rozvinutější je cirkulační struktura bočních válců. Materiál (písek), unášený ze dna silným proudem vodního skoku v blízkosti podélné osy koryta, je zčásti odnášen pryč z oblasti výmolu a zčásti je cirkulován v bočních válcích. Pohyb jednotlivých částic písku v cirkulačních oblastech probíhá od středu proudu do stran ke svahům, odsud podél bočních svahů protiproudně a zpětně je nasáván do hlavního proudu v ose koryta.
Jakmile se tento cirkulační splaveninový proces ustálí, začne se další vývoj maximální hloubky výmolu zpomalovat. Hlavní proud má již totiž částečně vyčerpanou transportní kapacitu materiálem, který je cirkulován v bočních válcích. Tento materiál zpětně vstupuje do hlavního proudu vždy, když jej proudění v bočních válcích posune u dna do osy koryta.
Někdy je šířka bočních válců již natolik velká, že zpětný proud podél svahů nemá dostatečnou sílu odebírat materiál ze dna. Výmol se prohlubuje více u středu, na okrajích se prohlubuje méně nebo vůbec. V takovýchto případech je dno na okrajích výmolové prohlubně velmi ploché a u středu koryta se příkře svažuje k místu maximální hloubky celého výmolu. Vytvářejí se zde postranní plošiny s jednou úzkou hlubokou prohlubní uprostřed profilu.
Hydraulická východiska studia výmolu
Jelikož v místě prostorového výmolu vzniká vodní skok, jehož charakteristiky je možno získat aplikací věty o hybnosti, lze zcela přirozeně uvažovat o tom, že i řešení prostorového výmolu bude vycházet z tohoto principu. Věta o hybnosti umožňuje přesné řešení při navrhování dimenzí vývarů konstantní šířky, pro případ prostorového výmolu tvaru hrušky je však šířka proměnná. Je potřeba počítat i s tlakovou normálovou silou, kterou je reakce stěn objektu „hrušky“, i když v případě deformovatelných stěn ani toto zcela neplatí. Půdorysně není rozměr vodního skoku z bočních stran vymezen pevnými stěnami, nýbrž kontaktními plochami s bočními válci (obr. 1 vpravo). Vzhledem k tomu, že v kontaktní ploše ze strany bočních válců se svislou osou má voda obvodovou rychlost danou prouděním ve víru, nelze počítat pouze s velikostí normálové síly, ale též s tečnou silou. Kromě toho nemusí být rozdělení tlaků ve vstupním profilu vždy hydrostatické a hybnost proudu ve výstupním profilu je v důsledku nerovnoměrného rozdělení rychlostí v příčném profilu ovlivněna i velikostí Boussinesqova čísla (poměr skutečné hybnosti proudu k hybnosti vyjádřené z průřezové rychlosti). Z předchozího je tedy zřejmé, že prostá aplikace věty o hybnosti nevede k cíli. Jako nadějnější se jeví návrh autora, jenž po vzoru Hunzingera [4] dává do vzájemné závislosti bezrozměrnou délku úplavu vznikajícího v rozšíření proudu:

a parametr F vzájemné přeměny kinetické a polohové energie v důsledku rozšíření (rov. 2).

Bezrozměrný parametr F definoval Ashida [1] vztahem:
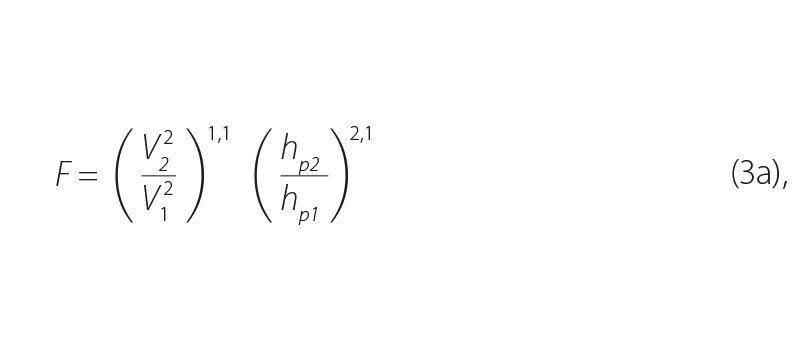
což je vyjádření přeměny energie v přechodové oblasti mezi vstupním profilem 1, kde je původní nezměněná šířka koryta, a profilem 2, kde je naopak šířka výmolu do stran největší. Důvod, proč by parametr energetické přeměny F mohl být dobrým indikátorem tendence k vytváření prostorového výmolu tvaru „hrušky“, plyne z úvahy, že čím více energie (kinetické i polohové) se přemění v bilančním úseku v disipativní formu energie a v část energie uplatňující se při transportu materiálu koryta, tím lze očekávat větší přetvárné účinky proudu na morfologii koryta, a tím bude i větší prostorový rozsah vzniklého výmolu. Všechny veličiny vystupující ve vztahu (rov. 3a) jsou uvedeny na obr. 3. V tomto definičním obrázku je význam uvedených hodnot následující:
- V1, V2 [m.s-1] –
průřezové rychlosti v příslušném profilu - A1, A2 [m2] –
průtočné plochy v příslušném bilančním profilu - c . A2 [m2] –
část průtočné plochy v profilu 2, zmenšená o recirkulační oblasti bočních vírů - H1 [m] – hloubka proudění v bilančním vstupním profilu 1
- hp1, hp2 [m] –
polohové výšky hladiny na vstupu do výmolu a v místě výmolu měřené od nejnižší úrovně dna výmolu - ∆HP = hp1 – hp2 [m] –
rozdíl polohových výšek hladin v bilančních profilech - Ys [m] –
hloubka výmolu „hrušky“ - Lw [m] –
celková délka výmolu „hrušky“ - B1, B2, B3 [m] –
šířky proudu v hladině na vstupu do výmolu, ve výmolu a těsně za výmolem
V rov. 3a je však uvažována jediná průřezová rychlost v celém profilu 1 a 2. Na základě vlastního výzkumu rozdělení bodových rychlostí v přechodové oblasti vývoje výmolu [5] lze doporučit modifikaci členů průřezových rychlostí v profilech 1 a 2 příslušnými koeficienty kinetické energie profilu (Coriolisovo číslo αe), zahrnujícími poměr skutečné kinetické energetické výšky k energetické výšce vyjádřené ze střední průřezové rychlosti.
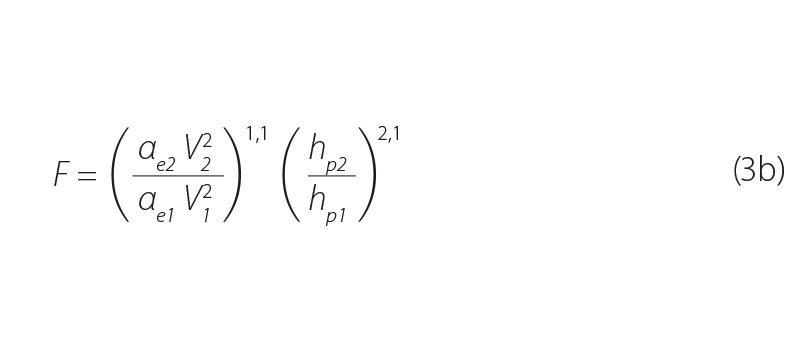
V bilančním vztahu (rov. 3b) je třeba věnovat zvláštní péči vhodné volbě polohy obou bilančních profilů – zejména pak profilu 2 (obr. 3).
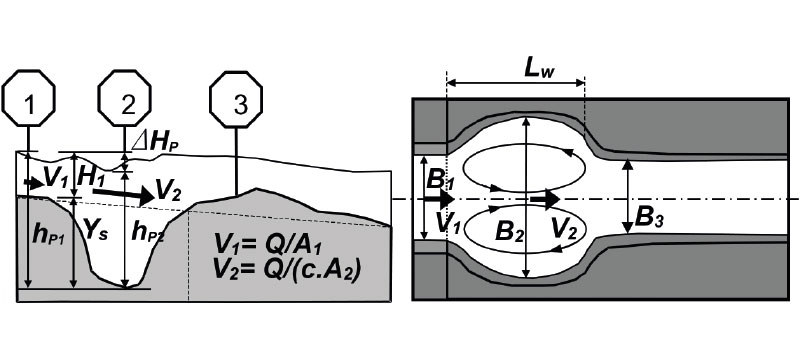
Obr. 3. Typická podoba výmolu „hrušky“ v podélném profilu (vlevo) a v půdorysu (vpravo) se základními rozměry vyznačenými v charakteristických profilech výmolu
Fig. 3. Typical form of the “pear” shaped scour hole in a long section (left) and a plan view (right) with basic dimensions marked at characteristic profiles of scour hole
Metodika stanovení změn koryta
Hlavním úkolem tohoto příspěvku je na podkladu předchozích sledování [5, 6] navrhnout jednoduchý postup pro stanovení rozměrů prostorového výmolu, jenž vzniká na přechodu od opevněného k plně rozvolněnému korytu bez jakéhokoli technického zajištění. Postup by měl být co nejjednodušší, umožňující určit rozsah morfologických změn koryta bez potřeby znalosti příliš mnoha detailů, které lze stanovit většinou jen v laboratorních podmínkách.
Vztahy pro stanovení základních rozměrů prostorového výmolu
Postup měření na „plném“ prostorovém modelu byl velmi pomalý a zdlouhavý. Nedařilo se zaměřovat časově si odpovídající průběhy hladiny a dna v podélném profilu a obou bilančních příčných profilech. Pro systematické měření bylo proto nutné přístup omezit na poloviční koryto. Veškerá vyhodnocovaná experimentální data v grafech na obr. 4 pocházejí právě z těchto měření.
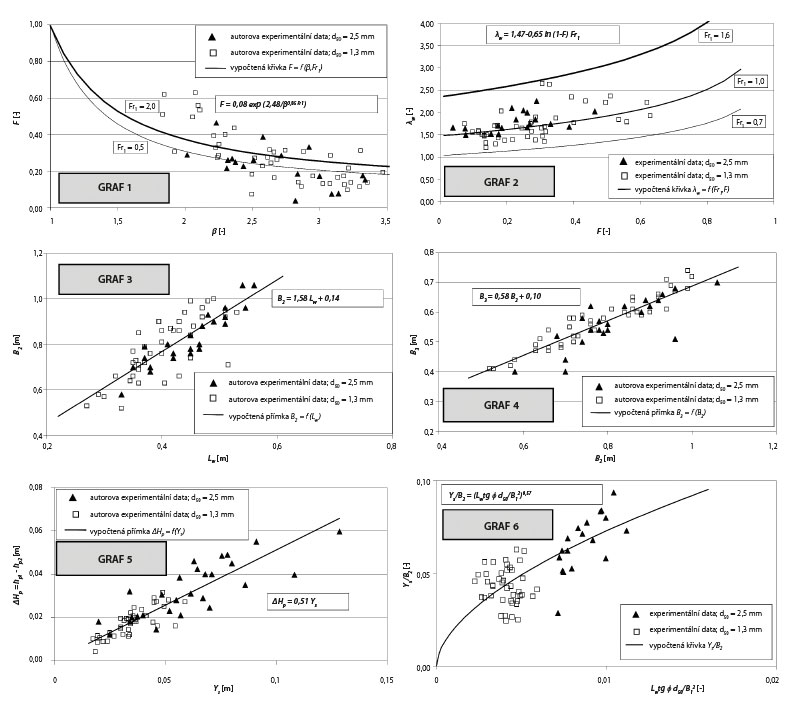
Obr. 4. Odvozené experimentální vztahy pro návrh výmolové prohlubně v přechodové oblasti rozvolněného koryta; grafy 1–6 jsou odkazovány ve schématu návrhu výmolové prohlubně (obr. 6)
Fig. 4. Relationships derived to design preformed scour hole at channel trasition; graphs 1–6 are referred in chart of design procedure of the scour hole (fig. 6)
Pro říčního inženýra není příliš praktické používat vzorec ve tvaru rov. 3b, např. kvůli nedostatku znalostí o rozložení lokálních rychlostí v profilu 1 a hlavně 2 (obr. 3), kde vznikají boční víry. Je třeba využít některé náhradní přímočařejší vztahy. Nabízí se vztah mezi F a β = B2/B1 vynesený na obr. 4 (graf 1). Je zřejmé, že F není pouze funkcí geometrických rozměrů výmolové prohlubně, ale souvisí také s vlastnostmi proudění před vstupem do přetvárného koryta. Proto je navržen vztah: F = F(β, Fr1), kde Fr1 je Froudovo číslo proudění ve vstupním úseku 1 definované vztahem Fr1 = V1/(gH1str )0,5, kde H1str je střední hloubka proudění, H1str = A1/B1, A1 je plocha proudění v bilančním profilu 1 a B1 je šířka proudění v hladině ve stejném úseku. Byl odvozen exponenciální vztah (rov. 4), který přirozeně splňuje logickou podmínku F = 1 pro poměr rozšíření koryta β = B2/B1 = 1.

Vztah získaný prokladem experimentálně zjištěnými body dosahuje součinitele determinace R2 = 0,867.
Dále byl z experimentálních dat (obr. 4 – graf 2) získán vztah mezi bezrozměrnou délkou úplavu λw v analogii s Hunzigerovým vztahem (rov. 2). Vztah zohledňuje závislost geometrických rozměrů, podílejících se na vyjádření bezrozměrné veličiny λw , na parametru energetické přeměny mezi profily 1 a 2, a navíc zohledňuje i podmínky (Fr1) na přítoku do přechodové oblasti koryta, kde se výmolová prohlubeň vyvíjí.
λw = 1,47-0,65ln (1-F) Fr1 (R2 = 0,978 – viz obr. 4 – graf 2) (5)
Zkušenosti z výzkumu tvaru výmolu, který vzniká účinkem ponořeného vodorovného paprsku na deformovatelné dno [2], ukazují, že tvar výmolu v jednotlivých okamžicích svého vývoje je podobný – afinní (obr. 5). Lze zjistit i zřejmou podobu mezi pozorovaným tvarem hladiny a dna v podélném profilu (obr. 1 vpravo). Proto je třeba hledat vztahy mezi základními geometrickými parametry výmolové prohlubně (B2, B3, Lw a Ys) a také mezi úrovněmi vodní hladiny (∆Hp = hp1 – hp2) a dna (Ys). Další odvozené vztahy (rov. 6 , 7 a 8) čerpané z experimentálně získaných dat (obr. 4 – graf 3, 4 a 5) byly určeny opět pomocí statistické analýzy [5, 6].
B2 = 1,58Lw + 0,14 (R2 = 0,992 – viz obr. 4 – graf 3) (6)
B3 = 0,58B2 + 0,10 (R2 = 0,978 – viz obr. 4 – graf 4) (7)
∆Hp = 0,51Ys (R2 = 0,923 – viz obr. 4 – graf 5) (8)
Poslední statisticky odvozený vztah z experimentálně získaných dat na „polovičním“ modelu rozvolněného koryta je patrný na obr. 4 z grafu 6.
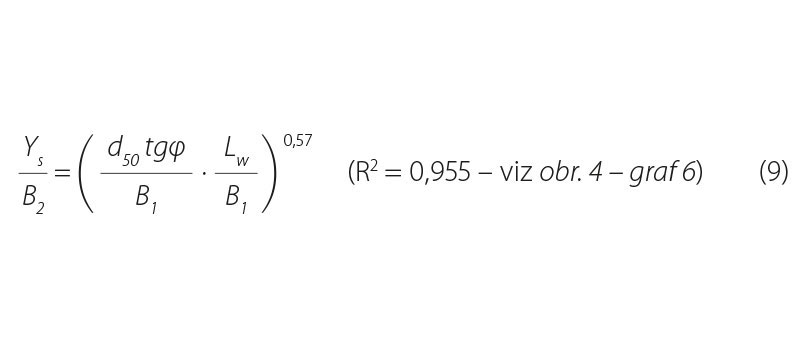
Autor si je vědom skutečnosti, že rov. 9 může mít i jiný než navržený tvar se zastoupením řady dalších kombinací bezrozměrných veličin. Z celé řady prověřovaných vztahů mezi bezrozměrnými veličinami byl dle [6] vybrán právě uvedený tvar na základě nejlepší dosažené kriteriální hodnoty optimalizačního procesu (R2) při zahrnutí minimálního počtu parametrů určených k optimalizaci (pouze mocninný exponent), což mělo pozitivní vliv na malou chybu v jejich hodnotě. Tato rovnice vzájemně svazuje všechny tři hlavní veličiny geometrie výmolu Lw, B2, Ys s veličinou B1 na vstupu do výmolu v závislosti na geomechanických vlastnostech zeminy (tg φ [-], d50 [m]).
Kromě definiční rovnice parametru energetické přeměny (rov. 3a) a navržených empirických rovnic (rov. 4–9) lze v souladu s obr. 3 ještě odvodit základní vazební rovnice pro polohové výšky v bilančních profilech 1 a 2.
hp1 = Ys + H1 (10)
hp2 = Ys + H1 – ∆Hp (11)
Poslední vazební rovnicí je výraz pro vyjádření bezrozměrné délky úplavu λw, kde Lw je délka úplavu odpovídající přibližně délce výmolové prohlubně.

Pro návrh rozměrů morfologického objektu byly odvozeny všechny potřebné kvantitativní vztahy. Všechny vztahy jsou rozměrově homogenní, jsou uvedeny ve formě závislosti geometrických rozměrů výmolové prohlubně (rov. 6, 7, 8, 10, 11) nebo závislosti bezrozměrných parametrů (rov. 3a, 4, 5, 9, 12). Tyto vzorce používají jako vstupní údaje hlavní geometrické a hydraulické charakteristiky vstupního proudu (B1, H1, V1, Fr1) v úseku koryta před rozvolněním toku a geomechanické vlastnosti nesoudržného materiálu v rozvolněné části (úhel sklonitosti zeminy pod vodou φ a reprezentativní velikost zrna zeminy d50). Je třeba upozornit, že v případě aplikace experimentálně odvozených rovnic je nutné vycházet z platnosti těchto vztahů pro určité rozmezí použitých bezrozměrných parametrů. Bezrozměrné vztahy (rov. 4, 5 a 9) byly odvozeny v rozmezí parametru Fr1 (0,75; 1,9) – tj. spíše v podmínkách charakteristických pro podhorské až horské potoky. Poměr rozšíření koryta β = B2/B1 ve výmolové prohlubni v experimentech odpovídal rozmezí (1,8; 3,5), tj. podmínkám proudění s dobře až velmi dobře rozvinutými bočními víry, které se výrazně podílejí na formování prostorového výmolu s charakteristickým tvarem „hrušky“. Bezrozměrné parametry výmolu byly v tomto rozmezí: B2/H1str (15; 50), Lw/H1str (7; 23)
a Ys/H1str (0,6; 2,7). Parametr energetické přeměny F se pohyboval v rozmezí (0,04; 0,8). Experimenty probíhaly pouze na dvou typech zrnitého nesoudržného lože, tvořeného významně stejnozrnnými ostrohrannými sklářskými písky FP 1–1,6 a FP 1,6–4 mm se zrnem d50 = 1,3 mm a 2,5 mm a s čísly nestejnozrnosti U = d60/d10 1,5, resp. 1,7. Specifická hmotnost písku byla pro oba případy 2 516 kg/m3 a objemová hmotnost 1 560 a 1 600 kg/m3. Úhel vnitřního tření pod vodou byl u jemnozrnnějšího písku 33,8° a u hrubšího písku 35,9°.
Změny všech relevantních geometrických rozměrů, jež jsou spojeny se vznikem a vývojem výmolu, jsou závislé na parametru, kterým je čas – lze tedy hovořit o „parametrickém výmolu“ [2]. V případě návrhu výmolu tvaru „hrušky“ jako stabilizovaného výmolu je třeba vycházet z jednoho známého rozměru výmolu. V praxi je častým omezením pro návrh výmolu typu „hrušky“ limitovaná šířka přilehlého příbřežního pásu, kde není nutné řešit komplikované vztahy s vlastníky okolních pozemků. Bude tedy volen tento limitovaný rozměr, odpovídající veličině B2; je možno však volit i kterýkoli z ostatních rozměrů (Ys, Lw). Touto volbou je do výpočtu vnesen nepřímo faktor času. Projektanta výmolu tvaru „hrušky“ nemusí zajímat, v jakém čase t by k vytvoření výmolu o výpočtem zjištěných dimenzích došlo. Podstatná je pro něj skutečnost, že jím zvolená dimenze výmolu (v čase t proměnná) je limitní, za niž již nelze jít, a že tvarově výmol odpovídá některému z afinních mezistavů (obr. 5), korespondujících s aktuálním rozsahem dvojice bočních vodních válců se svislými osami. Výmol typu „hruška“ je pak třeba ve výpočtem stanovených dimenzích stabilizovat, např. zapuštěnými záhozovými žebry ve dně i na svazích na začátku a konci objektu. Konkrétní technické opatření stabilizace výmolu však musí vycházet z místních zvyklostí na daném vodním toku, respektujících zejména charakter zemin v nivních uloženinách a dostupnou materiálovou základnu.
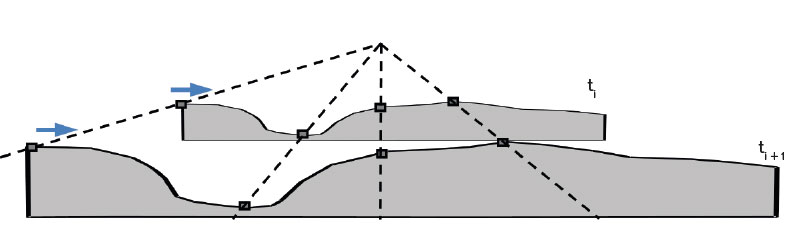
Obr. 5. Parametrický vývoj tvaru výmolu – tvar výmolu pro jakýkoli časový okamžik t je afinní ke tvaru v jiném časovém okamžiku t + 1
Fig. 5. Parametric scour hole development – the scour hole shape for any time instant t is affine to the shape at another time instant t + 1
Návrhová metodika prostorového výmolu
Schéma postupu stanovení základních rozměrů výmolové prohlubně v přechodové oblasti rozvolněného koryta vychází z grafického znázornění na obr. 6. Pro vstupní tvarově fixovaný profil 1 opevněného koryta jsou známy charakteristiky proudu – hloubka H1, rychlost V1, hodnota Froudova čísla Fr1 a šířka proudu B1 odpovídající výchozí šířce koryta v přechodové oblasti rozvolněného koryta. Návrh výmolové prohlubně jako prostorového morfologického prvku spočívá v určení jeho základních geometrických rozměrů B2, Lw, Ys, B3 a stanovení snížené průřezové rychlosti V2 v rozšířeném profilu 2 (obr. 3). Postup stanovení základních veličin výmolu se u alternativy a), b) nebo c) na obr. 6 liší podle toho, zda je výchozím známým nebo zadaným rozměrem výmolové prohlubně její maximální šířka B2, hloubka Ys, nebo délka Lw. Ve všech alternativách výpočtu je třeba nejdříve určit poměr rozšíření koryta β = B2/B1 – pokud B2 není známo nebo zadáno, je třeba jej odhadnout. Dále je třeba dle grafu 1 nebo ze vztahu (rov. 4) stanovit parametr energetické přeměny F v závislosti na β a hodnotě Fr1 a dle grafu 2 nebo ze vztahu (rov. 5) bezrozměrnou délku úplavu λw, jež spojuje základní půdorysné rozměry výmolové prohlubně Lw, B1 a B2 prostřednictvím vztahu (rov. 12). Pokud B2 nebylo známo na počátku výpočtu a bylo nutné ho volit, lze jeho správnou volbu ověřit právě vztahem (rov. 12), popř. i grafem 6, resp. vztahem (rov. 9), který spojuje geomechanické vlastnosti nesoudržného materiálu v rozvolnění koryta a všechny základní geometrické rozměry výmolové prohlubně. Pokud je docíleno dostatečné shody odhadu B2 s jeho hodnotou určenou výpočtem, lze postupovat dále stanovením šířky koryta na konci výmolové prohlubně B3 dle grafu 4, resp. pomocí vztahu (rov. 7). Pokud je třeba stanovit průřezovou rychlost V2 v profilu 2 (např. pro posouzení kritické nevymílací rychlosti částic dna), stanoví se nejdříve snížení hladiny ve výmolu ∆Hp dle grafu 5, resp. vztahem (rov. 8) a následně se využijí vazební vztahy (rov. 10) a (rov. 11) ke stanovení polohových výšek hp1 a hp2. Poté již lze použít definiční vztah (rov. 3a) pro stanovení průřezové rychlosti V2 v profilu 2 ve výmolu.
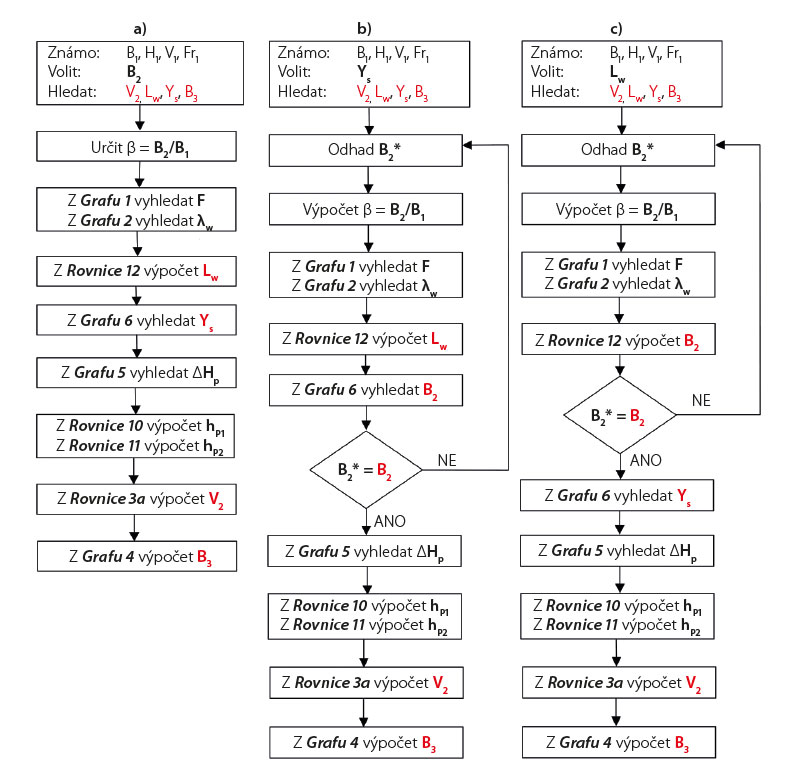
Obr. 6. Schéma postupu stanovení prostorové výmolové prohlubně, kdy jeden z rozměrů je zvolen: a) B2 je zvolen; b) Ys je zvolen; c) Lw je zvolen. Odkazované grafy jsou uvedeny v obr. 4, čísla rovnic odpovídají textu
Fig. 6. Charts of design procedure of the scour hole dimensions which one is chosen: a) B2 is given; b) Ys is given; c) Lw is given. The referenced graphs are shown in fig. 4, the numbers of the referenced formulas correspond to the text
VÝSLEDKY A DISKUZE
Soustava empirických rovnic (4–9) společně s rovnicemi výškových vztahů (10, 11) a definičními vztahy (3a) a (12) tvoří systém k plnému řešení prostorového výmolu tvaru „hrušky“. Vzájemně provázaná aplikace jednotlivých vztahů při výpočtu výmolu, tvořící ucelený postup, je chápána jako metodika návrhu výmolu typu „hruška“. Každá z empirických rovnic však byla statisticky upřesněna pouze individuálně. Je tedy nezbytné prověřit, jaké míry shody s měřenými daty lze docílit při aplikaci celého systému navržených vztahů – návrhové metodiky. Nejedná se zde o verifikaci na nezávislém souboru dat. Jde pouze o prověření, jak „přiléhavá“ je celá metodika výpočtu výmolu v porovnání s měřenými daty, z nichž byl každý z použitých empirických vztahů individuálně odvozen. Při stanovení výmolu typu „hruška“ musí být vždy jeden z rozměrů výmolu volen, čímž je do návrhu parametrického výmolu vnesen faktor času. Podle toho, který z rozměrů je volen, musí být metodický postup mírně upraven – jsou použity stejné vztahy, ale v jiném pořadí. Schémata postupu řešení pro případ, že jsou voleny rozměry a) B2, b) Ys, nebo c) Lw, jsou uvedena na obr. 6.
Postup posouzení „přiléhavosti“ probíhal následovně. Vyšlo se ze známých údajů o proudění na vstupním profilu do výmolu (průřezová rychlost V1, hloubka H1 a šířka proudu B1 a z nich stanovená hodnota Fr1) a geomechanických vlastností zeminy (d50, ϕ ) – tyto údaje budou většinou v praxi také známy. Byly aplikovány jednotlivé postupy řešení podle toho, který z rozměrů B2, Ys nebo Lw byl volen jako výchozí pro výpočet. Výsledkem byly vypočtené veličiny B2, Lw, Ys, ∆HP, V2, B3 (označené indexem comp = computed). Ty byly porovnány pomocí testu shody s veličinami změřenými v polovičním modelu koryta (označené indexem meas = measured). Výsledky testu shody pro výpočet při zvoleném rozměru B2 ukazuje obr. 7. První graf sady vykazuje naprostou shodu, neboť zaměřená data byla použita zároveň i jako výchozí rozměr ve výpočtu. Provedené testy shody pro další volené výchozí rozměry výmolové prohlubně Ys a Lw (není zobrazeno) umožňují učinit závěr, že výpočetní metodika výmolu je „nejpřiléhavější“, pokud je jako výchozí volený rozměr pro výpočet použita právě šířka výmolu B2.
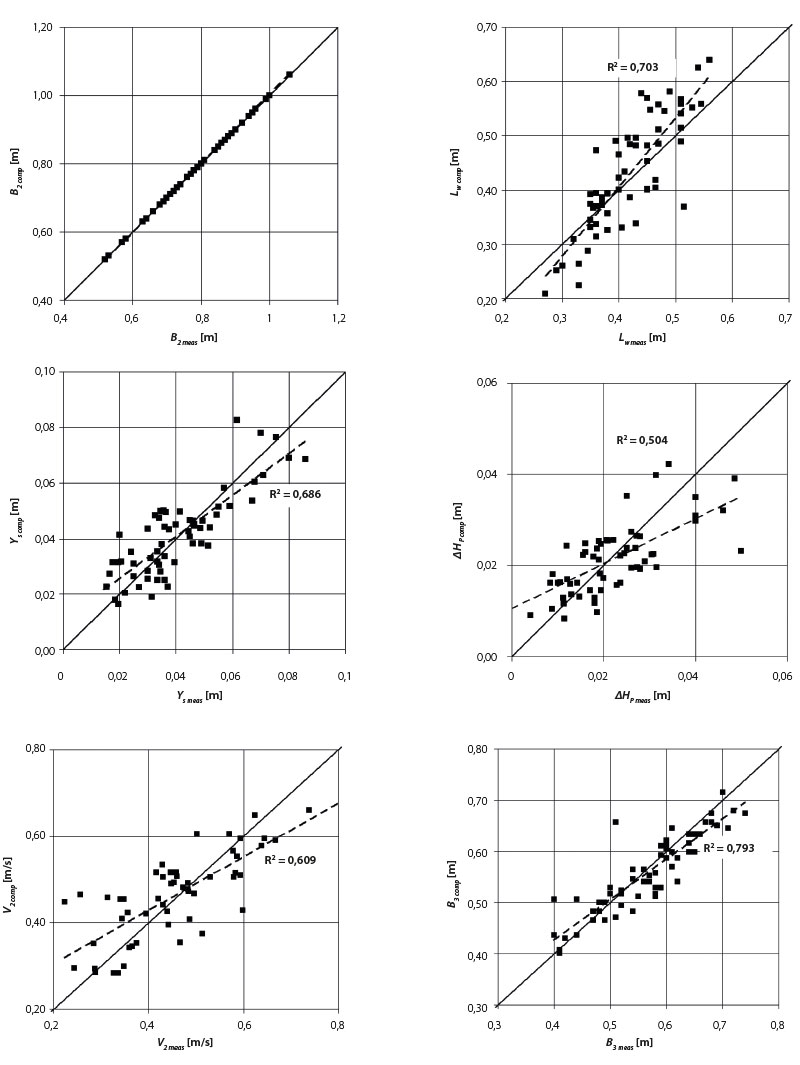
Obr. 7. Posouzení přiléhavosti metodiky výpočtu výmolu testem shody vypočtených (comp) a měřených (meas) geometrických a hydraulických charakteristik při volbě šířky B2
Fig. 7. Assessment of the scour hole computation procedure suitability by testing the agreement between calculated (comp) and measured (meas) geometric and hydraulic characteristics when the width B2 is given
Mimo posouzení „přiléhavosti“ u navržené výpočetní metodiky byla také provedena její verifikace se skupinou nezávislých dat, jež byla získána na „úplném“ prostorovém modelu. Ze sady 23 experimentů na prostorovém modelu bylo možné vyhodnotit jen některé posuzované veličiny s četností hodnot v souboru v rozmezí 4–17. Toto porovnání mezi výpočetní metodikou odvozenou na „polovičním“ modelu a daty zjištěnými v „úplném“ prostorovém modelu je jistě užitečné (obr. 8). Lze zde stanovit, jak významně se promítne zjednodušující předpoklad symetrie proudění ve výmolu do správnosti výpočetní metodiky odvozené za zjednodušujících předpokladů.
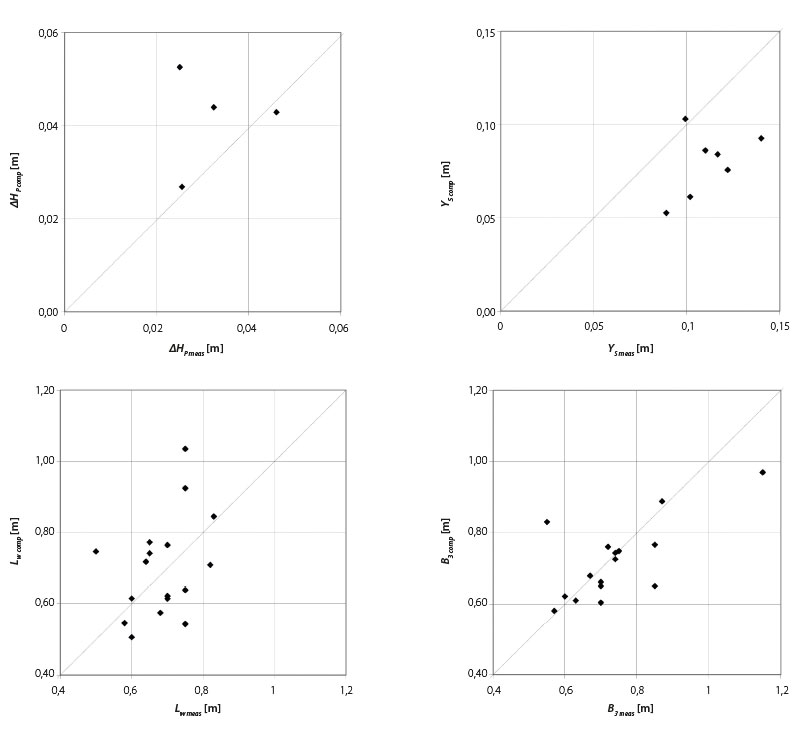
Obr. 8. Verifikace výpočetní metodiky návrhu výmolu typu „hrušky“ (při voleném B2) testem shody s daty zjištěnými na „plném“ prostorovém modelu
Fig. 8. Verification of the “pear shaped“ scour hole computation procedure (when B2 is given) by a test of agreement with the data measured in the “full” spatial model
Dat pro porovnání je málo. Ta, která byla k dispozici, ukazují, že zjednodušující předpoklad symetrie skutečně má určitý dopad na přesnost navržené metodiky výpočtu výmolu typu „hrušky“ při její aplikaci na plně prostorový případ vymílání. Lze se však domnívat, že ovlivnění správnosti výpočetní metodiky z důvodu předpokladu symetrie proudění nepřesahuje vliv jiných faktorů, včetně chyb při měření. Např. svislicové rychlosti určené v „polovičním“ modelu byly měřeny zjednodušeným způsobem a skleněná stěna v ose proudu zřejmě mírně ovlivňovala tvar hladiny i dna v její blízkosti. Naopak u „plného“ modelu docházelo k méně přesnému a časově nepohotovému zaměřování dna a hladiny hrotovým měřítkem. Při zvážení všech uvedených vlivů zahrnutých v rámci chyb a zkreslení při zvoleném postupu experimentálních prací se lze domnívat, že předložená výpočetní metodika má reálné jádro a mohla by být přínosem v oblasti návrhu morfologických objektů při revitalizačních úpravách na vodních tocích.
ZÁVĚR
Výše uvedený postup pro stanovení prostorové výmolové prohlubně v rozvolnění toku lze využít při návrhu přírodě blízkých koryt malých vodních toků nebo v procesu zpřírodňování v minulosti necitlivě kanalizovaných koryt drobných vodotečí v podhorských oblastech. Konstruování předem vytvořených morfologických objektů ve formě cíleného rozvolnění koryta, které podporují vznik prostorového proudění a disipaci přebytku kinetické energie, může být užitečným a nákladově efektivním opatřením v prevenci proti destruktivní erozi povodňového průtoku v korytě a zároveň může vést ke zvýšení morfologické, a tedy i habitatové rozmanitosti uvnitř koryta vodního toku.
Nicméně, přijetí těchto opatření v rámci procesu revitalizačních úprav koryta vodního toku musí být vždy řádně posouzeno příslušným vodoprávním úřadem z hlediska změny stavu i užívání vlastního koryta a území v okolí vodního toku, kdy se např. opevněný meliorovaný odvodňovací kanál změní na tvarově rozvolněný mělký luční potok a okolní odvodněná zemědělsky využívaná plocha se přemění na občasně zatápěné louky.
Poděkování
Příspěvek vznikl v rámci řešení projektu podpořeného Technologickou agenturou ČR SS02030027 „Vodní systémy a vodní hospodářství v ČR v podmínkách změny klimatu (Centrum Voda)“.
Příspěvek prošel lektorským řízením.
DOI: 10.46555/VTEI.2023.07.002