ABSTRAKT
Tato studie je zaměřena na výpočet parametru α zvlhčovací větve retenční křivky a na vliv jeho hodnoty na účinnost kapilárních bariér. Kapilární bariéra je jednoduchou metodou odizolování skládek. Efektivita kapilárních bariér byla testována pomocí numerických modelů, které umožňují větší variabilitu testování oproti fyzikálnímu měření. Díky numerickým modelům bylo možné vyhodnocovat přímý vliv změny parametrů retenčních křivek na fungování kapilárních bariér. Do sestavování numerických modelů byla zahrnuta hystereze retenčních křivek a následně byl vyhodnocen její vliv na shodu výsledků modelů s měřenými daty. Numerické modelování je vhodným a spolehlivým nástrojem při ověřování účinnosti kapilárních bariér. Vzhledem k citlivosti výsledků na parametry úlohy je zapotřebí určit co nejpřesněji všechny nutné vstupní parametry, aby měl výsledný model reálnou vypovídací hodnotu.
ÚVOD
Kapilární bariéra, případně v kombinaci s dalším objektem [1], je efektivním nástrojem využívaným při zakrývání skládek a k ochraně určité oblasti proti proniknutí podzemní vody. Její princip je založen na odlišných hydraulických vlastnostech dvou půdních vrstev, zpravidla různých písků nebo písku a štěrku. Jemnozrnnější nadložní vrstva složená z jemně až střednězrnného písku se nazývá kapilární vrstva. Spodní vrstva skládající se z hrubozrnnějšího materiálu, obvykle střednězrnného štěrku, se nazývá kapilární blok. Rozhraní mezi kapilární vrstvou a kapilárním blokem se označuje jako kapilární rozhraní. Hydraulická vodivost kapilární vrstvy je při určitých tlakových podmínkách vyšší než hydraulická vodivost kapilárního bloku. To platí pro nižší tlakové výšky, při nichž je kapilární blok téměř nepropustný. Díky tomu dochází k odtoku vody kapilární vrstvou spíš než k jejímu proniknutí do kapilárního bloku [2, 3]. V některých případech je pro zvýšení účinnosti nebo pro větší zabezpečení jednoduchá kapilární bariéra doplněna geotextilní vrstvou vloženou na kapilární rozhraní. Takto sestavené kapilární bariéry se nazývají kombinované [4, 5]. Kombinovaná bariéra se používá pro případ selhání jednoduché kapilární bariéry.
Evropská směrnice (Směrnice Rady 1999/31/ES) vyžaduje k zakrytí skládek odpadu třídy II použití dvou nezávislých komponent. To se zpravidla zajišťuje umělou a minerální vrstvou. Alternativou je užití umělého těsnění (geotextilie) v kombinaci s kapilární bariérou. V tomto případě se umělá vrstva může umístit nad nebo pod kapilární bariéru, TASi (německá zkratka pro Technickou direktivu o komunálních skládkách – Technische Anleitung zur Verwertung, Behandlung und sonstigen Entsorgung von Siedlungsabfällen) však doporučuje vložit umělé těsnění mezi kapilární blok a kapilární vrstvu. Takto vytvořená kombinovaná kapilární bariéra je ve srovnání s klasickým kombinovaným těsněním levnější, konstrukčně výhodnější a méně náchylná k poškození konsolidací. Zůstává pouze požadavek minimálního sklonu [6–8, 1].
Základem matematického modelu proudění vody v obecně nenasycené zóně je Richardsova rovnice. Rovnice samotná ale nestačí, abychom správně formulovali problém; je třeba dodat dva konstituční vztahy, jimiž jsou hydraulická vodivost a retenční křivka. Vzhledem k tomu, že retenční křivku můžeme v jistém smyslu, tj. při zahrnutí hystereze, považovat za prostou funkci, máme dvě možnosti: difuzní a kapacitní formu Richardsovy rovnice. Většinou bývá vhodnější kapacitní forma, s níž budeme nadále pracovat.
Obecně není retenční křivka jednoduchou funkcí; pro vztah mezi tlakovou výškou a vlhkostí je charakteristická hystereze. Při navrhování a testování kapilárních bariér bývá hystereze zanedbána [4, 9], podrobnější studie však ukazují, že má nezanedbatelný vliv na jejich účinnost [10–13].
Experimentální stanovení retenční křivky není jednoduché; zpravidla se určuje pouze hlavní drenážní větev. Mnohem náročnější měření zvlhčovací větve nebývá k dispozici. Použijeme-li při modelování proudění drenážní větev retenční křivky, nadhodnotíme účinnost bariéry. Vzhledem k tomu, že k zatěžování kapilárního rozhraní – a k jeho případnému prolomení – dochází při vzrůstající vlhkosti v kapilární vrstvě, je správnější zahrnout do modelu hysterezi. Níže podrobně uvádíme, jakým způsobem jsme do použitých matematických modelů zvlhčovací větev implementovali.
Tato studie se zaměřuje na určení parametru α pro zvlhčovací větev retenční křivky (ozn. αw) a na jeho vliv na účinnost kapilárních bariér. Kromě standardně využívaného vztahu mezi parametry α zvlhčovací a drenážní větve, αw = 2αd [14], bylo využito i analogie na základě výsledků měření drenážní i zvlhčovací větve retenční křivky, které provedla Trpkošová [15]. Výpočtem parametru αw se zabývali Likos et al. [16], když z výsledků experimentů se zvlhčovací větví určili van Genuchtenovy parametry α, m a n.
K testování efektivity kapilární bariéry při odlišných hodnotách parametru α slouží numerické modelování. Vzhledem k náročnosti experimentálního testování kapilárních bariér se využívá opakovaně prokázané skutečnosti, že matematické modely jsou dostatečně účinné a přesné k tomu, aby spolehlivě simulovaly experimentální měření, viz např. [1, 17–20]. Pomocí separátních modelů pro hlavní drenážní a hlavní zvlhčovací větev retenční křivky bylo dále možné vyhodnotit případný vliv hystereze na fungování kapilárních bariér.
Hydromechanické charakteristiky prostředí
K numerickému modelování proudění vody v kapilárních bariérách užíváme kapacitní formu Richardsovy rovnice ve dvou prostorových proměnných. Využitými konstitučními vztahy jsou hydraulická vodivost K(h) a retenční křivka ve tvaru θ(h), kde h je tlaková výška a θ je vlhkost.
Richardsova rovnice je pak vyjádřena následovně:
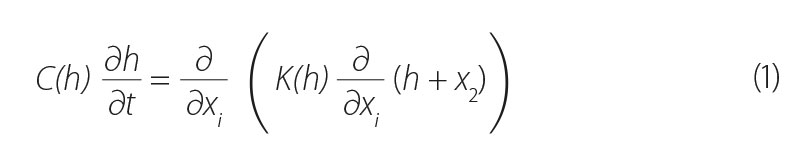
kde:
C(h) = ∂θ / ∂h [L-1] je kapacitní funkce
t [T] čas
x1, x2 [L] kartézské souřadnice
osa x2 orientována svisle vzhůru
Retenční křivka je rovnovážný konstituční vztah udávající hodnotu vlhkosti v závislosti na tlakové výšce. K jejímu vyjádření se obvykle využívá van Genuchtenův vztah [21]:

kde:
θr a θs [-] jsou reziduální a nasycená vlhkost
α [L-1], m [-] a n [-] van Genuchtenovy parametry
Obecně platí α > 0, m ε (1; 0) a n > 1. Zpravidla navíc předpokládáme m = 1 – 1/n.
Pro stanovení těchto parametrů z měřených dat retenční křivky slouží program RETC [22].
V numerických simulacích prováděných v rámci této studie byl k vyjádření závislosti hydraulické vodivosti na tlakové výšce použit obvyklý distribuční model:
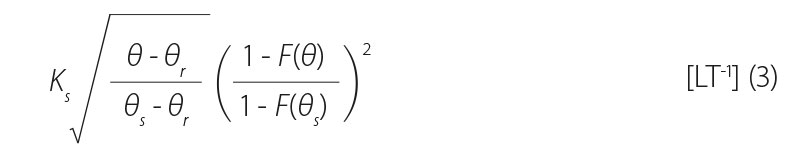
kde:
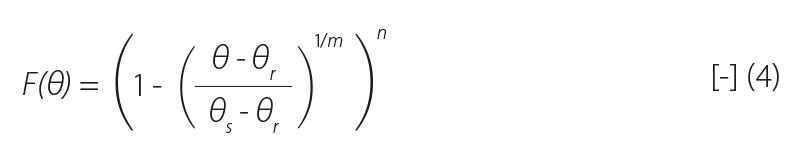
viz [23, 21].
Do kapacitní formy Richardsovy rovnice vstupuje hydraulická vodivost ve tvaru:
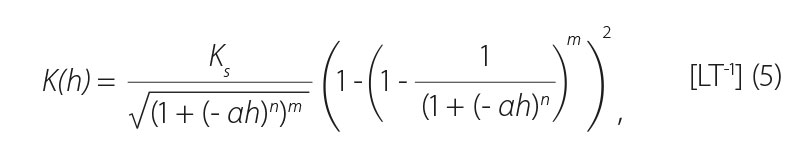
který dostaneme dosazením vhodné větve retenční křivky (2) do rovnice 3.
Průběh zvlhčování a průběh odvodňování nejsou dány jedinou funkcí. Obecná změna vlhkosti závisí na probíhajícím procesu (rostoucí nebo klesající tlaková výška) a na hodnotách vlhkosti a tlakové výšky v bodech obratu; zavedení hystereze do matematického modelu proudění znamená ztrátu jednoznačnosti funkce θ(h). Jednoduchý, a přitom dostatečně spolehlivý model hystereze je prezentován v článku [24]. V modelu je využito zjednodušení θrd = θrw = θr, nd = nw = n a αd < αw [25]. Zde a dále horními indexy d a w označujeme drenážní a zvlhčovací větve. Autoři do rovnice 2 také zavádějí nenulovou vstupní hodnotu vzduchu podle [26], vztah αw = 2αd a předpoklad, že během zvlhčovacích fází nedochází k uzavírání vzduchu v pórech, tj. že platí θrd = θrw = θr. Drenážní, resp. zvlhčovací větve vyšších řádů retenční křivky pak dostávají jednoduchou lineární transformaci založenou pro daný bod obratu na rozdílu hodnot aktuální vlhkosti a vlhkosti dané hlavní drenážní větví pro aktuální tlakovou výšku, resp. na rozdílu hodnot aktuální vlhkosti a vlhkosti dané hlavní zvlhčovací větví pro aktuální tlakovou výšku. Pro potřeby tohoto článku je důležité, že navržená metoda dává v případě hlavní drenážní a hlavní zvlhčovací větve nejen rozdílné vstupní hodnoty vzduchu, ale i rozdílné hodnoty tlakových výšek inflexního bodu obou větví.
V této studii považujeme retenční křivku za jednoznačnou funkci danou hlavní zvlhčovací větví. To odpovídá výše uvedené skutečnosti, že kritickým procesem v kapilární bariéře je rostoucí tlaková výška. Protože v každé fázi reálného procesu je při dané hodnotě tlakových výšek vlhkost rovna nebo vyšší než vlhkost udávaná hlavní zvlhčovací větví, může být hydraulická vodivost kapilární vrstvy daným zjednodušením poněkud podhodnocena, a tím může být podhodnocena i účinnost kapilární bariéry. Porovnání výsledků s experimenty, jež byly k dispozici, však ukazuje velmi dobrou shodu a potvrzuje spolehlivost použité metody. Toto zjištění je navíc v souladu se závěry uvedenými v publikaci [24].
METODIKA
Studované materiály a jejich parametry
Pro účely této studie byla převzata jedna reálná, dobře zdokumentovaná kapilární bariéra, která slouží jako standard pro srovnání s dalšími variantami, a byl vygenerován jeden hypotetický materiál jako vhodná alternativní kapilární vrstva. Takto získané tři základní materiály, dvě různé kapilární vrstvy a jeden kapilární blok, pak byly využity k vytvoření několika možných variant hlavních zvlhčovacích větví (stále s možností srovnání s měřenou zvlhčovací větví) generovaných podle pravidel uváděných v odborné literatuře. Výchozí materiály kapilární vrstvy a kapilárního bloku byly převzaty z dokumentace experimentálního testování kapilární bariéry provedeného na Ruhrské univerzitě v Bochumi [27] a laboratorního měření použitých materiálů provedeného na Přírodovědecké fakultě UK [1, 28]. Pro kapilární blok jde o homogenní materiál (dále označovaný B0) s velikostí zrn 2–8 mm. Podle Powersovy klasifikace [29] náleží do kategorie „slabě zaoblený“; částice mají dobře zaoblené hrany a hůře zaoblené vrcholy. Pro kapilární vrstvu se jedná o materiál (dále označovaný L0) vzniklý v říčním prostředí, z něhož byly vápnité části a větší zrna odstraněny. Podle Powersovy klasifikace náleží do kategorie zaoblený, částice mají zaoblené jak hrany, tak vrcholy.
Pomocí tenzní aparatury navržené podle Havlíčka a Myslivce [30] byly naměřeny drenážní i zvlhčovací větve retenčních křivek u obou materiálů. Díky tomu bylo možné získané charakteristiky použít pro porovnání numerických výsledků s výsledky laboratorních měření ve sklopném žlabu a následně, po potvrzení spolehlivosti numerických simulací, pro vyhodnocení vlivu hystereze při matematickém modelování kapilárních bariér. Hlavní drenážní, resp. hlavní zvlhčovací větev materiálu kapilární vrstvy označujeme nadále Lod, resp. L0w. Podobně hlavní drenážní větev a hlavní zvlhčovací větev kapilárního bloku označujeme B0d a B0w.
Pro další studium vlivu parametrů kapilární vrstvy na účinnost bariéry byl pomocí softwaru Rosetta [31] vygenerován vlastní materiál kapilární vrstvy označený L1 a definovaný souborem parametrů θr, θsd, αd, nd tak, aby těmito parametry určený materiál svými zrnitostními vlastnostmi odpovídal požadavkům na materiál kapilární vrstvy podle Píchy [2].
Nenasycená hydraulická vodivost testovaných materiálů byla určena pomocí vztahu (5), s nasycenou vodivostí Ks = 1,18 × 10-4 m/s převzatou z materiálu L0.
Hydraulické vodivosti materiálů L1 a B1 kapilární vrstvy a bloku odpovídající drenážním větvím retenčních křivek jsou uvedeny na obr. 1. V grafu je vidět, jak se obě funkce liší a jak se jejich rozdíl mění s měnící se tlakovou výškou.
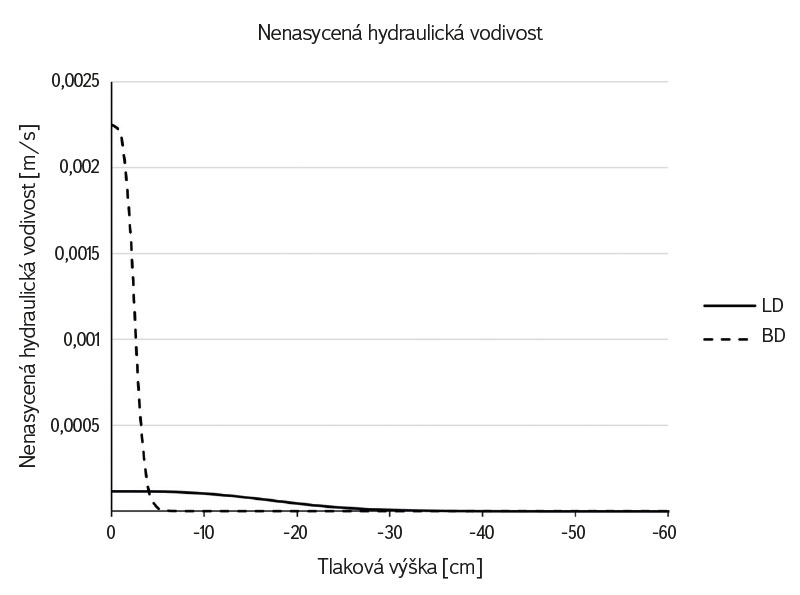
Obr. 1. Nenasycená hydraulická vodivost kapilární bariéry. Křivky závislosti nenasycené hydraulické vodivosti na tlakové výšce pro kapilární vrstvu LD a kapilární blok BD. Data odpovídají drenážní větvi retenční křivky
Fig. 1. Unsaturated hydraulic conductivity of the capillary barrier. The curve of dependence unsaturated hydraulic conductivity on the pressure head for capillary layer LD and capillary block BD. The data correspond to the drainage branch of the retention curve
Vzhledem k tomu, že obecně nelze v matematickém modelu kapilární bariéry zanedbat hysterezi a pracovat pouze s hlavní drenážní větví, věnujeme se v této studii podrobněji konstrukci hlavní zvlhčovací větve z obvykle měřených parametrů drenážní větve, konkrétně možnosti změny pouze parametru α [14, 24].
Obecně platí αw > αd. Byly posuzovány dva základní přístupy pro určení parametrů αw. V prvním případě byly využity výsledky laboratorního měření z předchozích studií [11] a vyhodnocena vzájemná souvislost parametrů α zvlhčovací a drenážní větve retenční křivky. Z výsledků měření vyplývá přepočtový vztah αw = 1,1αd pro kapilární blok a αw = 1,4αd pro kapilární vrstvu. Dále byl zkoumán výše citovaný vztah αw = 2αd podle Scotta et al. [14].
Vstupní parametry numerických modelů pro drenážní i zvlhčovací větve retenčních křivek studovaných materiálů kapilární bariéry jsou shrnuty v tab 1.
Tab. 1. Parametry testovaných materiálů
Tab. 1. Parameters of the tested materials
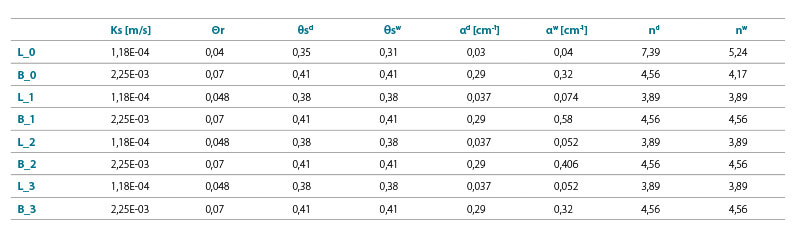
K získání parametrů αw a nw ze známých parametrů αd a nd jsme tedy zvolili zjednodušení nd = nw navržené ve studii Dohnala et al. [24], kde je porovnáním numerických simulací s experimentálním měřením potvrzena jeho dostatečná přesnost. Z uvedených dat vyplývá, že byly měněny pouze hodnoty parametru α pro zvlhčovací větev retenční křivky. Varianta č. 1 odpovídá použití vztahu αw = 2αd podle [14]. Pro variantu č. 2 byly využity přepočtové vztahy αw = 1,4αd pro kapilární vrstvu i blok. Ve variantě č. 3 byly uvažovány vztahy αw = 1,4 αd pro kapilární vrstvu a αw = 1,1αd pro kapilární blok. Retenční křivky studovaných materiálů odpovídající zmíněným variantám parametru αw kapilární vrstvy a kapilárního bloku bariéry jsou graficky znázorněny na obr. 2 a 3. Jsou v nich patrné rozdíly mezi drenážními a zvlhčovacími větvemi.
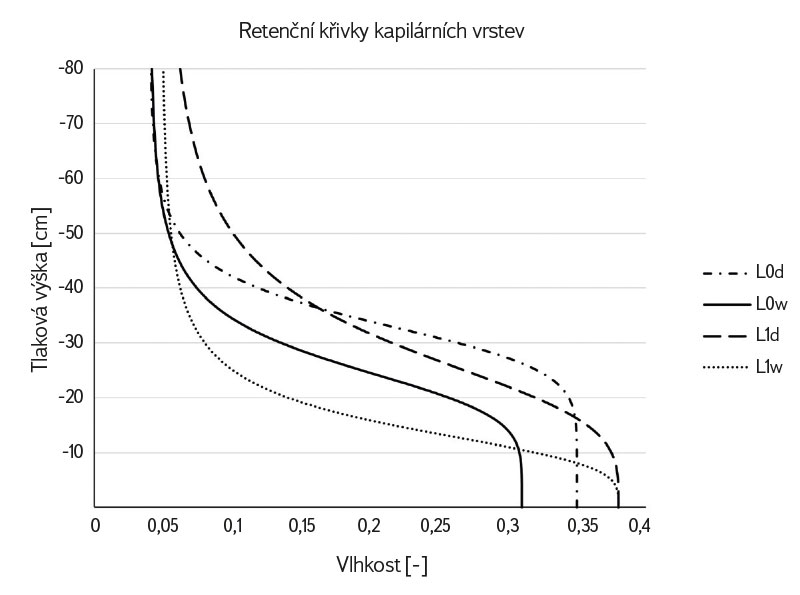
Obr. 2. Hlavní drenážní a hlavní zvlhčovací větve retenčních křivek reálného (L0) a vygenerovaného (L1) materiálu kapilární vrstvy
Fig. 2. Main drainage and main wetting branches of the retention curve of real (L0) and composed (L1) capillary-layer materials
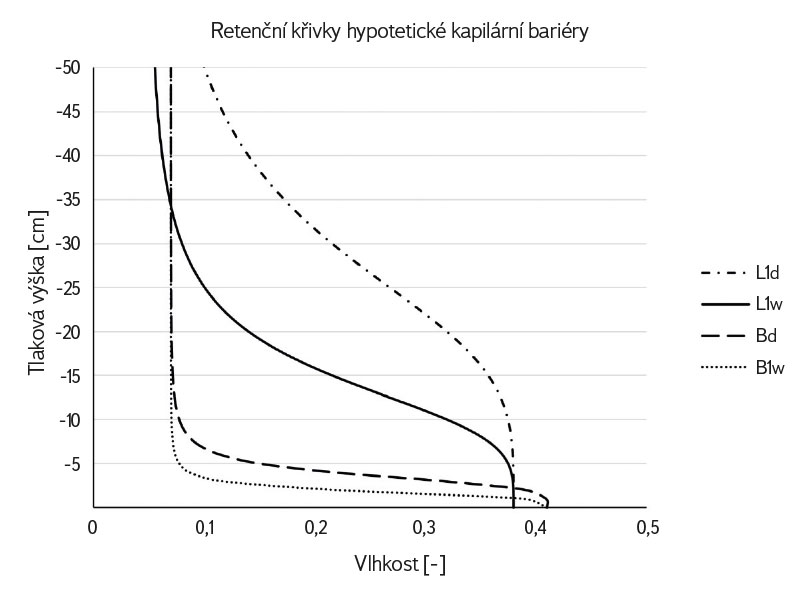
Obr. 3. Hystereze retenčních křivek kapilární vrstvy a kapilárního bloku hypotetické kapilární bariéry. Křivky L1d a Bd znázorňují drenážní větev retenčních křivek kapilární vrstvy a kapilárního bloku, L1w a B1w zobrazují zvlhčovací větev retenční křivky kapilární vrstvy a kapilárního bloku
Fig. 3. Retention curve hysteresis of capillary layer and capillary block of the hypothetical capillary barrier. Curves L1d and Bd represent the drainage branch of the retention curves of the capillary layer and the capillary block; L1w and B1w depict the wetting branch of the retention curves of the capillary layer and the capillary block
Na obr. 4 jsou pro srovnání vykresleny zvlhčovací větve retenční křivky kapilárního bloku podle změny parametru αw.
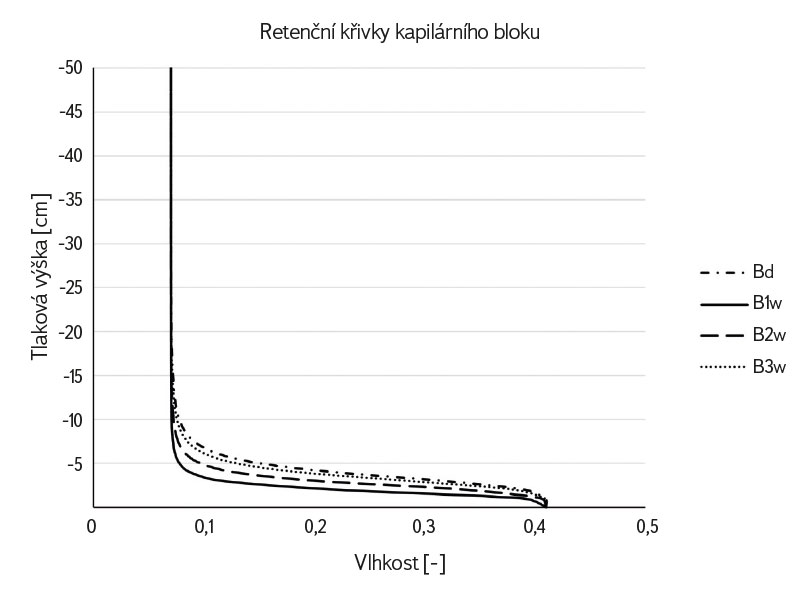
Obr. 4. Retenční křivky kapilárního bloku s odlišnými hodnotami parametru αw. Porovnání retenční křivky kapilárního bloku pro drenážní větev BD a tří variant B1w, B2w a B3w pro zvlhčovací větev reflektující změnu parametrem αw
Fig. 4. Capillary block retention curves with different values for parameter αw. Comparison of the capillary block retention curves for draining branch BD and the three variants B1w, B2w and B3w of the wetting branch reflecting the changes in the parameter αw
Vliv parametru α na modely kapilárních bariér
Parametr α můžeme považovat za rozhodující faktor k vyjádření změny retenční křivky při změně procesu z vysoušení na zvlhčování a naopak. Experimentálně naměřená data hlavních zvlhčovacích větví materiálů B0 a L0 [1] umožnila určit užitím programu RETC parametry těchto hlavních zvlhčovacích větví. Kromě efektu zavřeného vzduchu byly zaznamenány, oproti příslušné hlavní drenážní větvi, změny nejen parametru α, ale i parametru n. To ovšem mohlo být způsobeno tím, že hlavní drenážní větev nebyla vzata v úvahu. Výzkum procesů, při nichž se opakovaně měnil směr změny vlhkosti [24], ukazuje, že matematický model zahrnující hysterezi užitím parametrů αd, αw a nd dává dostatečně přesnou simulaci procesů zahrnujících oba směry změny vlhkosti.
Jelikož jsme se zaměřovali na vliv volby parametru αw na účinnost kapilární bariéry, pracovali jsme s numerickými modely několika variant této volby. Matematické modely byly formulovány ve dvou prostorových proměnných (ve svislém řezu vedeném spádnicí bariéry). K výpočtům byl použit program S2D_dual [32], který řeší kapacitní formu Richardsovy rovnice metodou konečných prvků. Pomocí numerických modelů bylo možné sledovat vývoj vsakujícího se postřiku v prostoru a čase v závislosti na měnících se parametrech. Byl sestaven model kapilární bariéry se základními hodnotami hydromechanických charakteristik. Počáteční tlaková výška byla nastavena na hodnotu -40 cm [1]. Okrajové podmínky se liší podle místa hranice. V místě infiltrace byla nastavena Neumannova okrajová podmínka odpovídající lineárně narůstající hodnotě postřiku, díky čemuž bylo možné porovnávat jednotlivé verze modelů a vyhodnotit čas prolomení kapilární bariéry ovlivněný měnícími se parametry. Odtok z kapilární bariéry byl modelován pomocí okrajové podmínky Seepage face v místech drenáže kapilární bariéry. Na zbývajícím okraji modelované oblasti, jež je reprezentována nepropustnou hranicí, byla nastavena nulová Neumannova okrajová podmínka. Okrajové podmínky jsou graficky znázorněny na obr. 5.
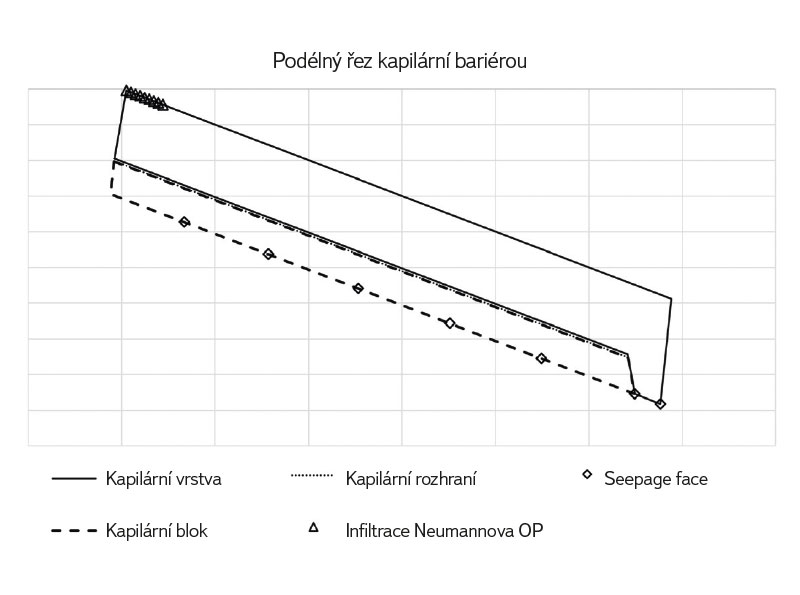
Obr. 5. Řez kapilární bariérou s vyznačenými okrajovými podmínkami pro infiltraci odpovídající nenulové Neumannově okrajové podmínce a okrajová podmínka drenáže z kapilárního bloku Seepage face. Na zbývající části hranice je nulová Neumannova okrajová podmínka. Délka kapilární bariéry je 6 m a výška 60 cm
Fig. 5. Section through the capillary barrier with marked boundary conditions for infiltration corresponding to the non-zero Neumann boundary condition and drainage from the capillary block as a Seepage face boundary condition. The remaining part of the boundary is the zero Neumann boundary condition. The length of the capillary barrier is 6 m and the height is 60 cm
Postřik byl pro všechny počítané varianty totožný, aby bylo možné výstupy mezi sebou porovnávat. Drenážní a zvlhčovací větve retenční křivky byly modelovány jako separátní verze modelů s odlišnými vstupními parametry. Bylo tedy možné vyhodnotit a ověřit vliv hystereze a volby parametru αw na fungování kapilárních bariér u všech modelovaných variant (obr. 6).
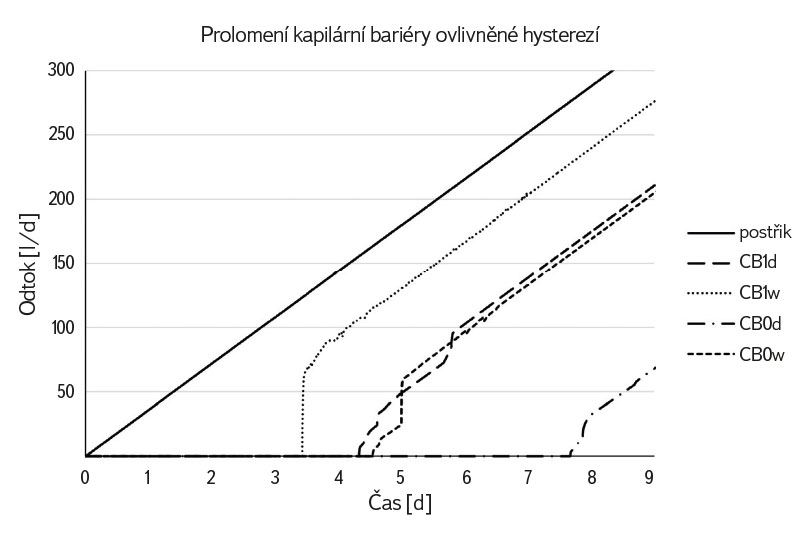
Obr. 6. Účinnost kapilární bariéry ovlivněná hysterezí. Graf znázorňuje lineárně narůstající postřik stejný pro všechny simulace, odtok z kapilárního bloku CB0d a CB0w pro drenážní a zvlhčovací větev retenční křivky výchozí kapilární bariéry a CB1d a CB1w pro drenážní a zvlhčovací větev retenční křivky varianty 1 hypotetické kapilární bariéry podle Scotta et al. [14]
Fig. 6. Capillary barrier efficiency affected by hysteresis. The graph shows linearly increasing irrigation (the same for all simulations), outflow from capillary block CB0d and CB0w for the drainage and wetting branch of the default capillary barrier retention curve, and CB1d and CB1w for the drainage and wetting branch of the retention curve of variant 1 of the hypothetical capillary barrier according to Scott et al. [14]
Kromě základní varianty modelu kapilární bariéry pro drenážní větve retenční křivky byly modelovány tři varianty pro zvlhčovací větve retenční křivky. Varianty výpočtu pro různé zvlhčovací větve jsou založeny na měnícím se parametru αw zvlhčovací větve retenční křivky kapilární vrstvy, případně i bloku. Výsledky jsou znázorněny na obr. 7.
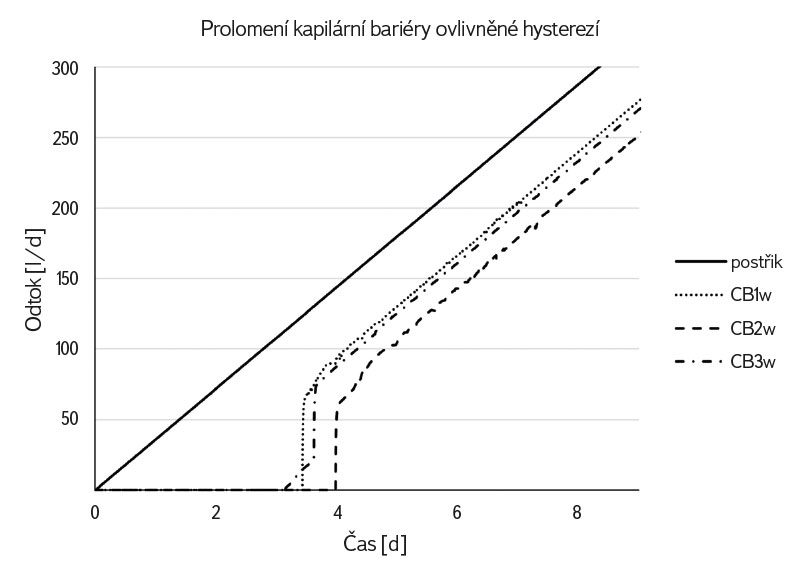
Obr. 7. Účinnost kapilární bariéry v závislosti na volbě parametru αw zvlhčovací větve retenční křivky. Postřik v grafu znázorňuje lineárně narůstající intenzitu postřiku, zvlhčovací křivky 1, 2 a 3 odpovídají odtoku z kapilárního bloku pro tři varianty výpočtu αw zvlhčovací větve retenční křivky
Fig. 7. Capillary barrier efficiency depending on the choice of parameter αw of the retention curve wetting branch. Irrigation in the chart shows a linearly increasing intensity of irrigation; wetting curves 1, 2, and 3 correspond to the outflow from the capillary block for three variants of calculation αw of the wetting branch retention curve
DISKUZE A ZÁVĚR
V této práci jsme srovnávali účinnost několika kapilárních bariér, jež se lišily kapilární vrstvou určenou testovanými volbami parametru α. Vzhledem k tomu, že pro výchozí materiál jsou k dispozici výsledky experimentálních testů, mohli jsme potvrdit, že matematický model bariéry dává dostatečně přesné výsledky už při použití samotné hlavní zvlhčovací větve. Srovnání s experimentálními výsledky dále ukázalo, že v případě účinnosti bariér nelze zanedbat hysterezi a pracovat pouze s drenážní větví kapilární bariéry. Byly tak potvrzeny předchozí experimenty [11, 28].
Série testů zaměřených na odvození hlavní zvlhčovací větve ve známých (tj. měřením určených) parametrech hlavní drenážní větve ukázala, že významnou roli v tomto kroku má určení parametru αw, a že je dokonce možné, jak navrhují citované publikace, zachovat parametry θrd, nd, případně i θsd, a hlavní drenážní větev definovat pouze vhodně určeným parametrem αw. Ukazuje se, že původně navrhovaná a v některých případech osvědčená volba αw = 2αd nemusí být tím nejlepším řešením. V případě výchozí bariéry B0, L0 je zřejmé, že takto zvolený parametr αw by mohl vést k podhodnocení účinnosti bariéry.
Ze získaných výsledků je patrné, že co nejpřesnější určení parametrů retenční křivky hraje podstatnou roli pro stanovení efektivity kapilární bariéry. Pokud máme dva fyzicky existující materiály, kapilární blok a kapilární vrstvu, a chceme zjistit účinnost jimi vytvořené kapilární bariéry, pak se můžeme spolehnout na test provedený matematickým modelem. Pro kapilární blok nám v takovém případě stačí parametry hlavní drenážní větve. Pro kapilární vrstvu, vzhledem k citlivosti výsledku na hodnotu parametru αw, je vhodné určit parametry hlavní zvlhčovací větve měřením. Pokud máme k dispozici jen parametry hlavní drenážní větve, je vhodné použít model hlavní zvlhčovací větve založený na změně pouze parametru α. Výsledky této studie ukazují, že v takovém případě je třeba volit pro αw vhodnou hodnotu v intervalu 1,1 αd ≤ αw ≤ αd.
Poděkování
Projekt „Hydromechanické charakteristiky retenčních křivek a jejich vliv na proudění podzemní vody” byl financován Grantovou agenturou Univerzity Karlovy pod č. 296215.
Příspěvek prošel recenzním řízením.
