Souhrn
Příspěvek prezentuje výsledky hydraulického výzkumu proudění mostním objektem s volnou hladinou a zatopeným vtokem na fyzikálním modelu. Srovnává dosavadní poznatky s naměřenými daty a diskutuje rozdíly. Příspěvek obsahuje analýzu tvorby zúžené hloubky za vtokem do mostního otvoru. Rovněž zpracovává závislost průtokového součinitele na řadě faktorů, jež je prezentována pomocí grafů a rovnic. Závěr práce dává doporučení pro volbu průtokového součinitele při výpočtech v softwaru Hec-Ras.
Úvod
Hydraulický výzkum proudění mostním objektem pro případ zatopeného vtoku a volného výtoku byl řešen na Fakultě stavební ČVUT v Praze v letech 2017 až 2019 v rámci projektu studentské grantové soutěže SGS17/171/OHK1/3T/11, jehož hlavní řešitelkou byla Ing. Petra Podešvová. Tento článek byl napsán za podpory tohoto projektu.
Základem řešení byl fyzikální výzkum, při kterém byl využit stávající skleněný žlab v hydraulické laboratoři fakulty. Vzhledem k rekonstrukci haly v posledním roce řešení byl výzkum doplněn i o simulace na 3D matematickém modelu.
Souhrn dosavadních poznatků
Výtok pod stavidlem
Proudění mostním otvorem se zatopeným vtokem a volným výtokem je blízké výtoku pod stavidlem. Charakteristický podélný profil hladiny pro případ výtoku pod stavidlem, kdy proudění není ovlivněno dolní vodou, je znázorněn na obr. 1.
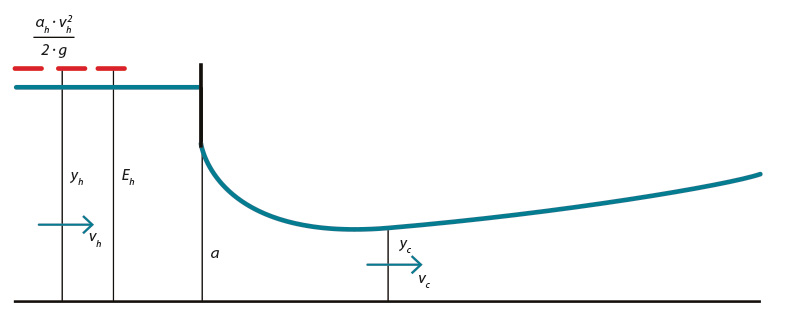
Obr. 1. Podélný profil hladiny při výtoku pod stavidlem neovlivněný dolní vodou
Fig. 1. Water level profile at sluice gate flow not affected by the downstream flow
Při nezatopení dolní vodou se vytváří zúžená hloubka yc ≈ 0,6a. Bernoulliho rovnice pro daný případ je:
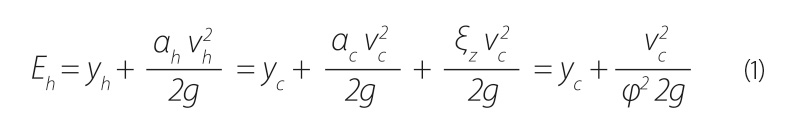
| kde | Eh [m] | je | energetická výška před vtokem do objektu, |
| yh [m] | hloubka před vtokem do objektu, | ||
| vh [m·s-1] | průřezová rychlost proudění před vtokem do objektu, | ||
| yc [m] | zúžená hloubka za výtokovým profilem, | ||
| vc [m·s-1] | průřezová rychlost v profilu zúžené hloubky, | ||
| a [-] | Coriolisovo číslo, | ||
| ξZ [-] | součinitel místní ztráty zúžením proudu, | ||
| φ [-] | rychlostní součinitel. |
Při uvažování:

| kde | a [m] | je | výška otvoru, |
| εv [-] | součinitel zúžení, |
po dosazení rovnice spojitosti do rovnice (1) a po zavedení výtokového součinitele dostaneme pro průtok:

| kde | b [m] | je | šířka otvoru, |
| kde | μv [-] | výtokový součinitel. |
Běžně publikované závislosti uvedených součinitelů na poměru yh/a jsou vykresleny na obr. 2.
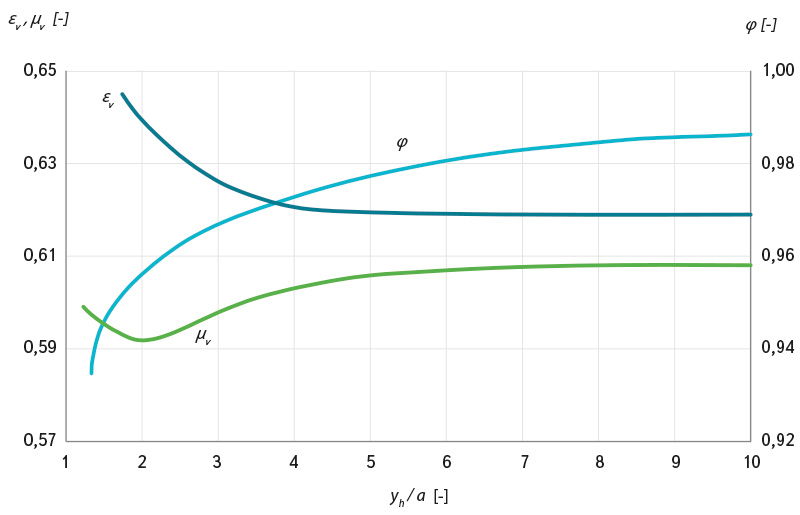
Obr. 2. Závislost součinitelů εv, μv a φ na poměru yh/a
Fig. 2. Dependence of coefficients εv, μv and φ on the ratio yh/a
Výpočet proudění mostním objektem se zatopeným vtokem a volným výtokem
Obdobné schéma a výpočtový postup jako pro případ výtoku pod stavidlem (rovnice (3)) bylo pro případ výpočtu proudění mostním objektem se zatopeným vtokem a volným výtokem publikováno Bradleym ve zprávě FHWA [1], zúžená hloubka yc je však uvažována jako polovina výšky mostního otvoru Hm/2. Podélný profil pro tento případ je vykreslen na obr. 3. Rovnice pro výpočet průtoku má tvar:
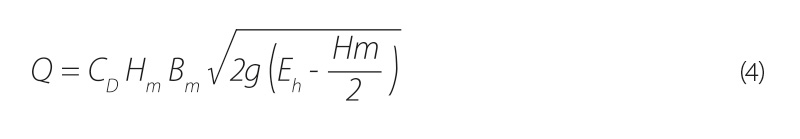
| kde | Q [m3·s-1] | je | průtok, |
| CD [-] | průtokový součinitel, | ||
| Hm [m] | světlá výška mostního otvoru, | ||
| Bm [m] | světlá šířka mostního otvoru (bez pilířů). |
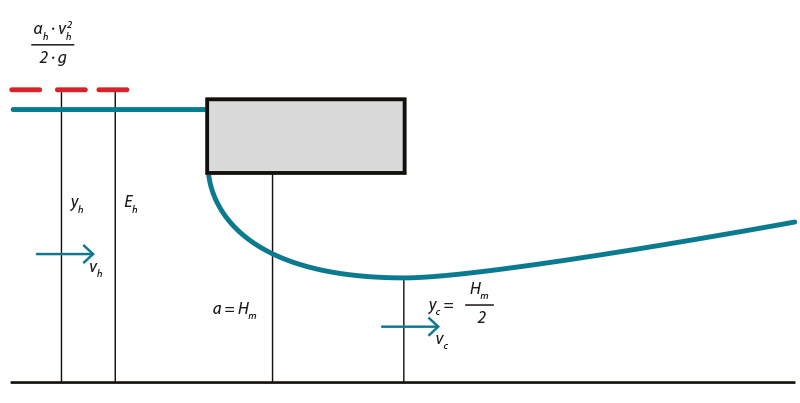
Obr. 3. Podélný profil hladiny při proudění mostním objektem se zatopeným vtokem a volným výtokem při uvažování yc = Hm/2
Fig. 3. Water level profile at bridge with free and submerged inlet when yc = Hm/2
V této publikaci je uveden graf závislosti průtokového součinitele CD na parametru yh/Hm, respektive na yh/yd, který je přiložen na obr. 4. Zde yd značí hloubku dolní vody. Průběh závislosti ukazuje, že proudění mostním objektem se zatopeným vtokem a volným výtokem pro hodnoty yh/Hm < 1,05 nemusí být stabilní, hodnota průtokového součinitele se v této oblasti pohybuje kolem hodnoty 0,3, s nárůstem velikosti poměrů se postupně zvyšuje až k hodnotě 0,5.
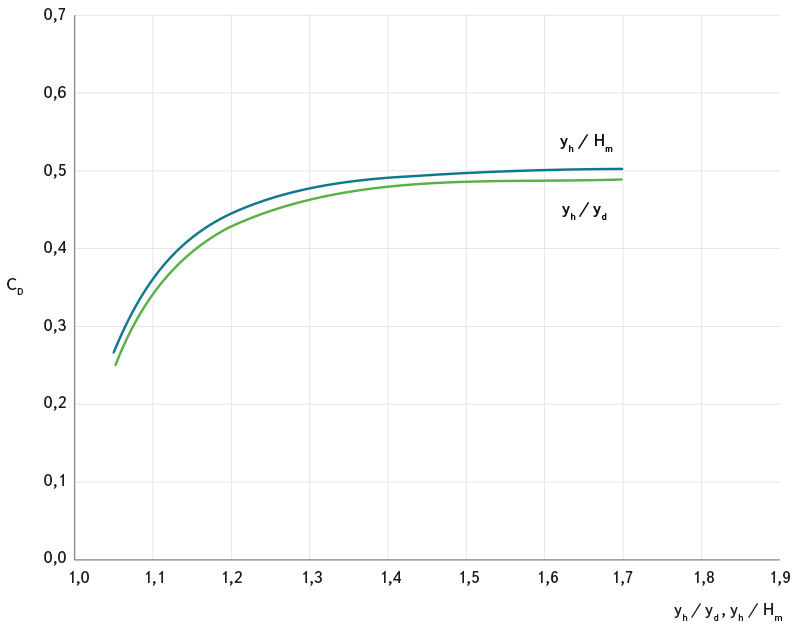
Obr. 4. Závislost průtokového součinitele CD na poměru yh/Hm a yh/yd podle Bradleyho [1]
Fig. 4. Dependence of discharge coefficient CD on ratio yh/Hm and yh/yd according to Bradley [1]
Rovnice (4) pro výpočet proudění mostním objektem se zatopeným vtokem a volným výtokem byla dále publikována v další publikaci FHWA [2], graf pro stanovení CD již však obsahuje jen závislost na yh/Hm s úpravou v oblasti hodnot yh/Hm < 1,08, graf je uveden na obr. 5.
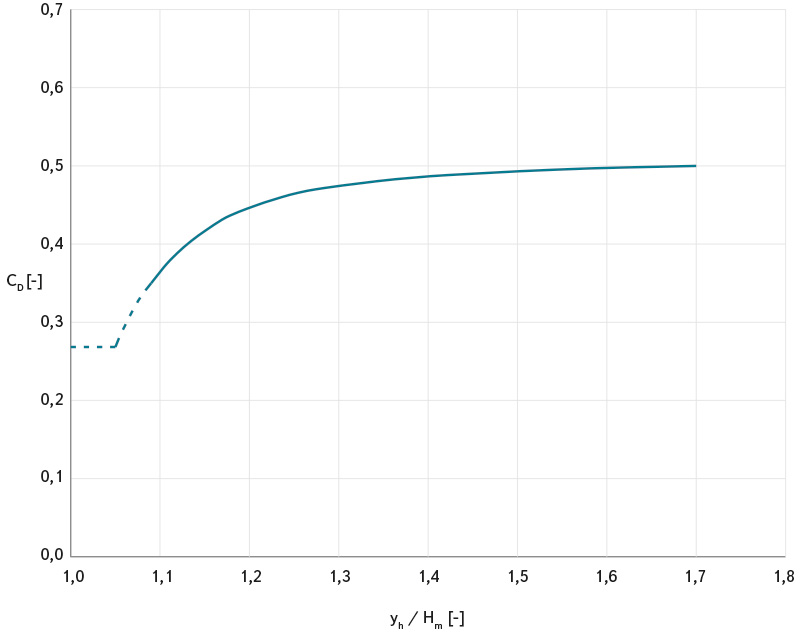
Obr. 5. Závislost průtokového součinitele CD na poměru yh/Hm podle Zevenbergena [2]
Fig. 5. Dependence of discharge coefficient CD on ratio yh/Hm according to Zevenbergen [2]
Rovnici (4) uvádí bez grafu ke stanovení CD ve své monografii Hamill [3], postup uvedený v publikaci [2] pak používá beze změny u nás hojně využívaný software Hec-Ras [4].
Výpočet tlakového proudění mostním objektem
Problematikou proudění mostním otvorem při tlakovém proudění se v rámci svého výzkumu velmi podrobně zabýval Picek [5]. Typický podélný profil hladiny pro tento scénář je zobrazen na obr. 6.
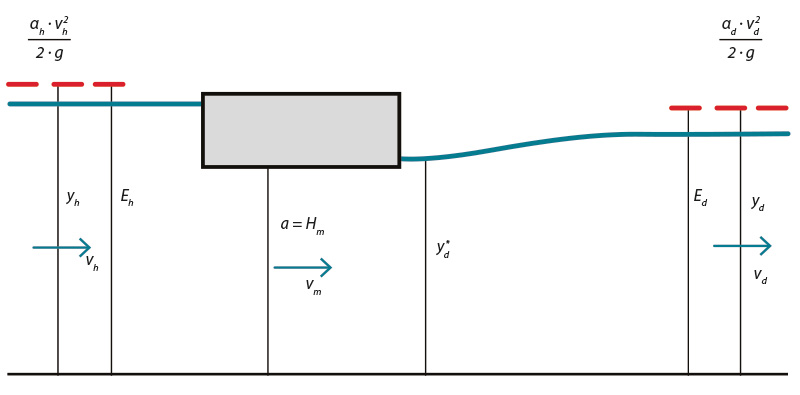
Obr. 6. Schéma podélného profilu pro případ tlakového proudění mostním objektem
Fig. 6. Water level profile at bridge with pressurized flow
Při zanedbání ztrát třením je možné při uvažování ztrát zúžením a následujícím rozšířením proudu napsat tuto Bernoulliho rovnici:
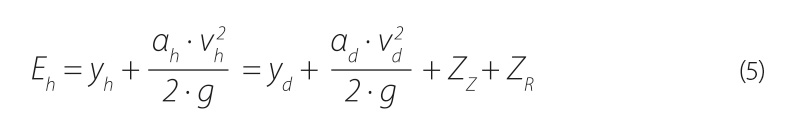
| kde | yd [m] | je | hloubka za výtokem z mostního objektu, |
| vd [m·s-1] | průřezová rychlost proudění v profilu za výtokem z mostního objektu, | ||
| ZZ [m] | ztráta zúžením na vtoku do mostního otvoru, | ||
| ZR [m] | ztráta rozšířením na výtoku z mostního otvoru. |
Ztráty zúžením je možné vyjádřit v závislosti na průřezové rychlosti ve vtokovém profilu mostu, ke stanovení ztrát rozšířením je možné použít více postupů (obdoba Bordovy ztráty pro náhlé rozšíření průměru potrubí jako funkci rozdílu rychlostních výšek na začátku a konci rozšíření proudu nebo analogie ztráty na výtoku do velké nádrže). Podrobně se touto problematikou ve své práci zabývala Jurečková [6]. Rovnici, která využívá poslední přístup, publikoval například Hamill [3]:

| kde | CD0 [-] | je | průtokový součinitel, |
| Sm = BmHm | plocha vtokového otvoru. |
Picek [5] však doporučuje pro druhý profil v Bernoulliho rovnici použít profil bezprostředně za výtokem z mostního otvoru, kde se vytváří hloubka yd* < yd, pro výpočet proudění tlakovým mostním objektem pak doporučuje užívat rovnici:

| kde | yd* [m] | je | hloubka těsně za výtokem z objektu (viz obr. 6). |
Vyhodnocení součinitele CD0 z experimentů na fyzikálním modelu podle obou rovnic je patrné na obr. 7.
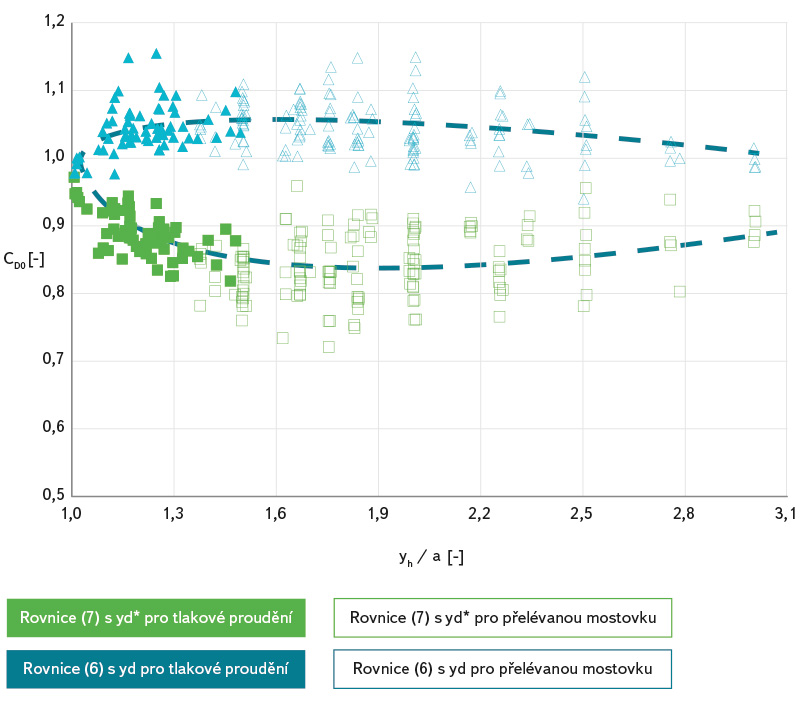
Obr. 7. Hodnoty průtokového koeficientu CD0 pro tlakové proudění vyhodnocené na základě experimentu podle rovnice (6), resp. (7)
Fig. 7. Values of discharge coefficient CD0 for pressurized flow obtained during the experiment according to the equation (6), respectively (7)
Metodika výzkumu
Modelová podobnost
Hydraulický výzkum byl založen na fyzikálním modelování při proudění s volnou hladinou. V tomto případě jsou dominantními silami síly gravitační a pro vyhodnocení se využívá Froudův zákon modelové podobnosti. Ten vyjadřuje skutečnost, že ve vzájemně příslušných profilech na modelu a ve skutečnosti budou stejná Froudova čísla. Bezrozměrné Froudovo číslo Fr je definováno rovnicí:

| kde | v [m·s-1] | je | průřezová rychlost proudění, |
| kde | y [m] | střední hloubka v profilu. |
Pro bezrozměrné veličiny, na které se při vyhodnocení výzkumu řešitelé zaměřili, ovšem platí, že hodnota z modelu má stejnou hodnotu i pro skutečnost.
Popis modelu
Výzkum byl prováděn ve Vodohospodářské hale Fakulty stavební ČVUT v Praze. Měření probíhalo v hydraulickém žlabu s nulovým podélným sklonem. Jeho rozměry byly následující: šířka 252 mm, délka 7 300 mm, výška stěn v první části 1 000 mm, v druhé části 500 mm. Začátek žlabu byl osazen voštinovým usměrňovačem pro rovnoměrné rozdělení proudu a na jeho konci byl umístěn žaluziový uzávěr sloužící k regulaci hloubky dolní vody.
Do žlabu byly postupně vkládány modely mostního objektu. Délka mostního objektu byla 100 mm a šířka mostního otvoru byla 130 mm, přičemž byly použity tři verze modelu lišící se světlou výškou mostního otvoru v rozměrech 80 mm, 100 mm a 120 mm. Jejich příčné řezy byly převzaty z diplomové práce Adély Dostálové [7] a jsou přiloženy na obr. 8.
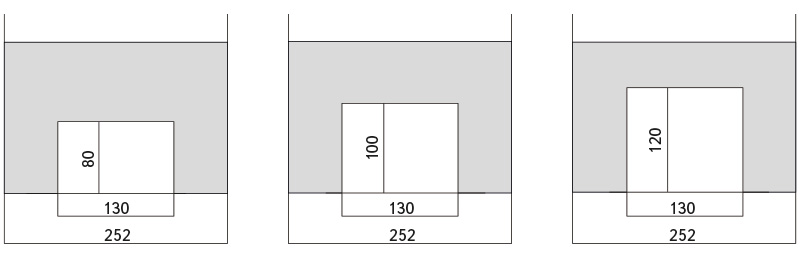
Obr. 8. Příčné řezy modelů mostních objektů včetně jejich rozměrů v [mm] [7]
Fig. 8. Cross sections of bridge models including their dimensions in [mm] [7]
Měření veličin
V rámci provedeného výzkumu byly měřeny pouze dvě veličiny, a to výška úrovní hladiny a průtok modelem. Úrovně hladin byly měřeny pomocí posuvného hrotového měřítka a hodnoty byly odečítány s přesností 0,1 mm. Pro měření průtoků byla použita dvě zařízení – indukční průtokoměr Magnetoflow Primo a měrný Thomsonův přeliv.
Během výzkumu bylo změřeno celkem 57 průběhů hladin. Pro každou variantu mostního objektu byly změřeny průběhy hladin pro čtyři hodnoty průtoku a pro každý z nich byly uvažovány čtyři varianty míry ovlivnění dolní vodou, celkem tedy 16 měření průběhu hladin. Na základě prvotního vyhodnocení bylo rozhodnuto o nutnosti doměření několika stavů zejména pro vyšší hodnoty průtoků na vtoku do mostního objektu.
Měření výšky hladiny bylo prováděno v bodech rozmístěných rovnoměrně v podélném a příčném směru, v blízkosti mostního objektu byla síť měřených bodů zhuštěna (viz obr. 9 převzatý z diplomové práce [7]). Ve většině příčných profilů bylo měření prováděno v pěti bodech, kdy jeden bod byl v ose proudění, další dva v jedné a třech čtvrtinách šířky od kraje žlabu a poslední dva body byly umístěny u kraje žlabu. Měřené body jsou znázorněny na obr. 9 červeně, zelenou barvou je zde znázorněno umístění mostního objektu.

Obr. 9. Síť měřených bodů v hydraulickém žlabu
Fig. 9. Mesh of the measured points in the hydraulic flume
Výsledky experimentálního výzkumu
Prohlídka rozsáhlého souboru dat, který byl během experimentálních prací pořízen, ukázala, že pro studium scénáře se zatopeným vtokem a volným výtokem bylo nezbytné ponechat jen některé pokusy, kdy se vyskytovala volná hladina pod celou délkou reálné mostní konstrukce. V souboru dat, který byl dále podroben statistické analýze, bylo ponecháno 34 průběhů hladin.
Typický průběh hladiny při experimentech je vykreslen na obr. 10. Za vtokovým profilem docházelo k postupnému snižování hladiny na hodnotu yc, v naprosté většině případů se tato hloubka objevovala přibližně ve vzdálenosti 2/3 délky mostního objektu. Pak se hladina postupně zvyšovala až k hodnotě yd.
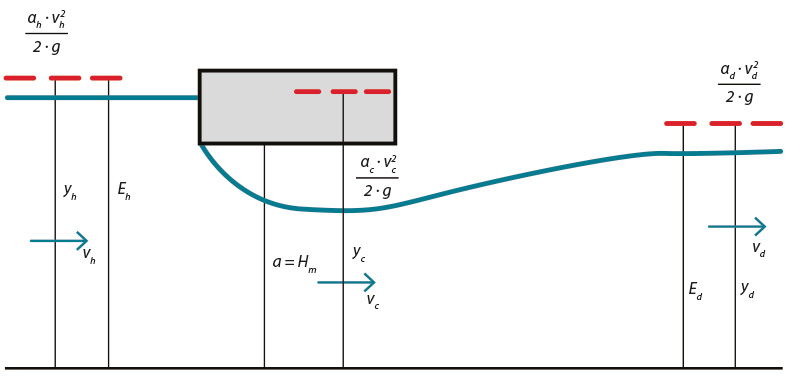
Obr. 10. Podélný profil hladiny vyskytující se při experimentálním měření
Fig. 10. Water level profile observed at the experimental measurements
Pro dané schéma je možné sestavit Bernoulliho rovnici mezi profilem zúžené hloubky yc a vzduté hloubky nad mostem yh ve tvaru (1) nebo mezi profilem s hloubkou dolní vody yd a vzduté hloubky nad mostem yh ve tvaru (5). Možnosti stanovení ztrát jsou popsány u rovnice (5), k vyčíslení ztrát je potřeba znát velikost rychlosti vc v profilu zúžené hloubky yc. V průběhu experimentů však rychlostní pole měřeno nebylo a řešitelé aktivní šířku proudění v zúženém profilu Bc pouze odhadovali na základě porovnání se simulacemi vybraných scénářů s využitím 3D matematického modelu. V rámci navazujícího výzkumu se počítá s tím, že se řešitelé zaměří právě na vyhodnocení rychlosti vc, která bude nezbytná pro vyhodnocení ztrát zúžením i rozšířením proudu.
Proto řešitelé v této fázi výzkumu zaměřili svou pozornost zejména na posouzení správnosti výpočtu vzduté úrovně hladiny nad mostem v případě zatopeného vtoku a volného výtoku podle přístupu Bradleyho. Zkušenosti s užíváním softwaru Hec-Ras, který tento postup používá, ukazují, že vypočítaná hloubka proudění nad mostním objektem yh dává v případě proudění se zatopeným vtokem a volným výtokem často vyšší hodnotu, než pro větší průtok, kdy je proudění objektem již plně tlakové. Rovnice využívá diskutabilní hodnotu zúžené hloubky za vtokem jako 0,5 · Hm, zatímco při výtoku otvorem to bývá podle obr. 2 cca 0,6 · Hm. Vyhodnocení experimentů pak ukázalo, že vytvoření průběhu hladiny se zatopeným vtokem a volným výtokem bylo dosaženo často jen při zatopení zúžené hloubky 0,6 · Hm dolní vodou. Tuto skutečnost dokládá graf na obr. 11.
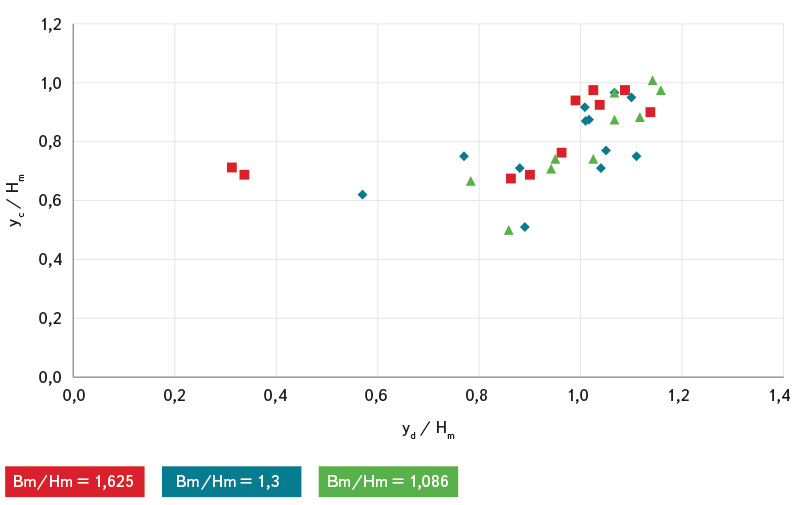
Obr. 11. Závislost poměru yc/Hm na yd/Hm pro provedené experimenty se zatopeným vtokem a volným výtokem
Fig. 11. Dependence of ratio yc/Hm on yd/Hm for experiments with free flow and submerged face of the deck
Na obr. 12 jsou zobrazeny hodnoty průtokového součinitele CD stanovené z rovnice (4) pro známé hodnoty Q, Eh, Hm a Bm stanovené vyhodnocením experimentů. Průběh bodů byl následně proložen křivkou, jejíž průběh je popsán rovnicí (9), fialovou čárou je pak vyznačen průběh Bradleyho závislosti. Pouhým okem je patrné, že naprostá většina hodnot součinitele CD je větší než podle Bradleyho.
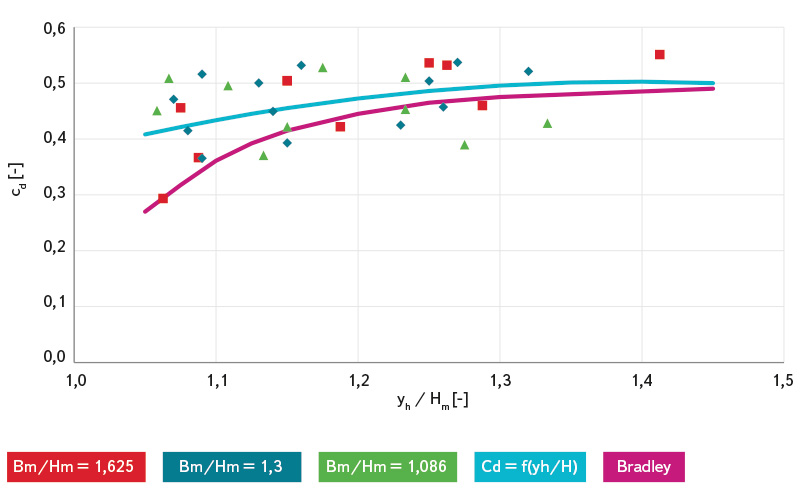
Obr. 12. Závislost průtokového součinitele CD na poměru yh/Hm
Fig. 12. Dependence of discharge coefficient CD on ratio yh/Hm
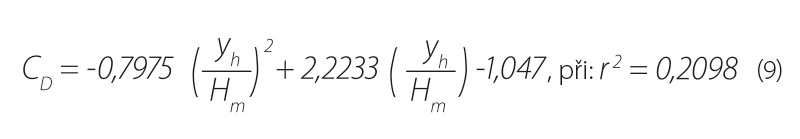
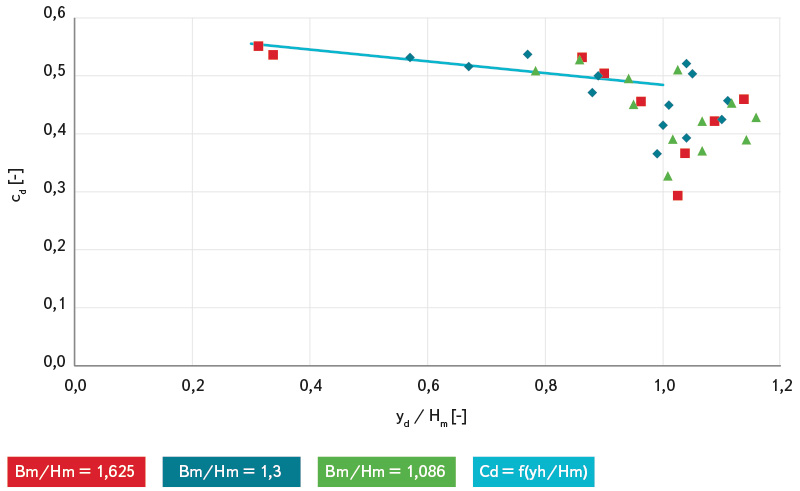
Obr. 13. Závislost průtokového součinitele CD na poměru yd/Hm
Fig. 13. Dependence of discharge coefficient CD on ratio yd/Hm
Jiný pohled na součinitel CD dává obr. 13, kde je zobrazena jeho závislost tentokrát na poměru yd/Hm. Vzhledem k tomu, že software Hec-Ras neumožňuje řešit podrobný průběh hladiny v profilu mostního objektu a v případě, že úroveň hladiny dolní vody je vyšší než spodní líc mostovky, program automaticky uvažuje tlakové proudění, byl průběh doplněn o proložení bodů s menšími hodnotami, než je yd/Hm < 0,97 lineární závislostí podle rovnice:
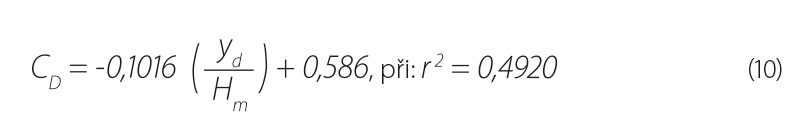
Na posledním obr. 14 je pak znázorněn průběh závislosti součinitele CD0, jehož hodnoty byly spočítány podle rovnice (6), na poměru yd/Hm. Zde je nezbytné uvést, že uvedená rovnice po fyzikální stránce nepopisuje proudění mostním objektem se zatopeným vtokem a volným výtokem zcela správně.
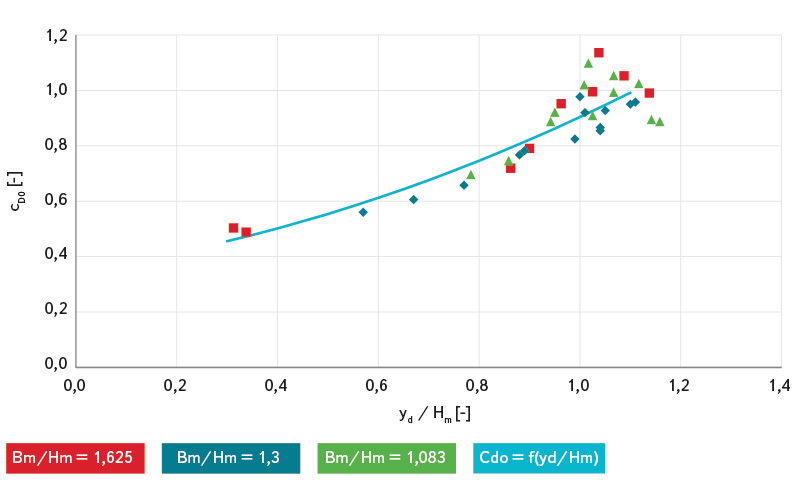
Obr. 14. Závislost součinitele CD0 stanoveného podle rovnice (6) na poměru yd/Hm
Fig. 14. Dependence of coefficient CD0 obtained from equation (6) on ratio yd/Hm
Průběh závislosti vykreslených bodů na obr. 14 byl proložen funkcí podle rovnice:
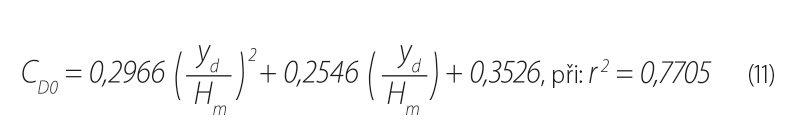
Jedním z dalších cílů řešitelů bude nalézt výpočetní postupy, které zajistí spojité řešení výpočtu vzduté hloubky nad mostem při přechodu ze stavu se zatopeným vtokem a volným výtokem na plně tlakové proudění, což software Hec-Ras neposkytuje. Porovnání grafu na obr. 14 s výstupy výzkumu Picka podle obr. 7 na možné propojení ukazují.
Závěr
Vyhodnocení experimentů na fyzikálním modelu při proudění mostním objektem se zatopeným vtokem a volným výtokem ukázaly na to, že výpočet vzduté hloubky nad mostem yh s využitím rovnice (4) a stanovením průtokového součinitele CD podle závislosti podle grafu na obr. 5 může dávat příliš velké hodnoty.
Na základě provedené analýzy zejména pak grafu na obr. 13 se v případě užití softwaru Hec-Ras doporučuje nepoužívat postup, kdy program sám odečte hodnotu CD z uvedené závislosti, ale doporučuje se pro hodnoty yd/Hm v rozsahu od 0,7 do 0,95 použít hodnotu CD = 0,5, pro hodnotu poměru menší než 0,7 přibližně CD = 0,525.
