Souhrn
Příspěvek prezentuje výsledky hydraulického fyzikálního výzkumu měrných přelivů pro měření malých, resp. minimálních průtoků. Výzkum se zaměřil na určení součinitelů přepadu pro nízké přepadové výšky. V příspěvku jsou uvedeny výsledky měření pro trojúhelníkový, obdélníkový a kruhový ostrohranný přeliv. Naměřená data jsou porovnávána se vztahy podle jednotlivých autorů a je určena vhodnost jejich použití pro oblast nízkých přepadových výšek. V rámci měření byly také provedeny pokusy s polokruhovou přelivnou hranou. Při laboratorním testování byly zkoumány rozdílné umístění přelivu vůči proudu a jejich vliv na výsledky měření.
Úvod
Pro kontinuální měření minimálních průtoků na malých vodních tocích lze použít měrné přelivy, které dokážou s velkou přesností měřit široký rozsah průtoků (obr. 1). Vlastní měření je realizováno nepřímo pomocí měření polohy hladiny nad měrným přelivem (pomocí tlakové sondy či ultrazvukového hladinoměru) a znalosti vztahu mezi výškou přepadového paprsku a odpovídající hodnotě průtoku. Vzhledem k častým suchým periodám a ke stále většímu tlaku na monitoring minimálních zůstatkových průtoků je přesnost měření minimálních průtoků na malých vodních tocích aktuálním tématem. Minimální či malý průtok lze pro námi zkoumanou oblast definovat v rozsahu jednotek litrů za vteřinu.

Obr. 1. Měrný přeliv osazený v terénu
Fig. 1. Measuring weir situated in the stream
Při měření malých, resp. minimálních průtoků ovšem nastává celá řada obtíží a problémů. Nízké průtoky přepadají přes přeliv s malou přepadovou výškou, při které již není hodnota součinitele přepadu v rozsahu platnosti používaných vzorců. Dále dochází k problémům se zanášením přelivů plávím, které může do značné míry zkreslit měřené průtoky.
V rámci laboratorního testování byly ověřovány hodnoty přepadového součinitele pro různé ostrohranné měrné přelivy a pro nízké přepadové výšky. Naměřená data byla porovnána s hodnotami podle rozlišných autorů a byla ověřena vhodnost jejich použití pro nízké přepadové výšky. Dále byla testována kruhová přelivná hrana a její vliv na kapacitu a chování přepadového paprsku. V rámci laboratorního testování byly zkoumány rozdílné umístění přelivu vůči proudu. Měrné přelivy byly vyrobeny metodou 3D tisku, která zajišťovala variabilitu a přesnost při výrobě různých tvarů přelivů.

Metodika experimentů
Veškeré laboratorní experimenty probíhaly v malé vodohospodářské hale Výzkumného ústavu vodohospodářského T. G. Masaryka, v. v. i., v pevném hydraulickém žlabu šířky 500 mm. Dodávka vody byla zajištěna pomocí čerpací stanice, která čerpala vodu z dolní nádrže do vysoko položené nádrže, jež zajišťovala stálou tlačnou výšku pomocí přelivu s dlouhou přelivnou hranou. Z této nádrže byla potrubím přivedena voda do žlabu. Průtok byl nastaven na základě velikosti otevření šoupěte na přívodním potrubí. Před vlastním vtokem do žlabu byl instalován Thomsonův měrný přeliv. Voda na konci žlabu byla odvedena odpadním potrubím do dolní nádrže.
Testovaný měrný přeliv byl při každém měření umístěn ve středu žlabu ve výšce 40 cm nade dnem žlabu (obr. 2). Testovaný přeliv byl umístěn cca 3,5 metru od nátoku do žlabu. Na nátoku do žlabu byl umístěn tlumič přitékající vody, který zajišťoval její uklidnění a rovnoměrný nátok do žlabu. Tlumič byl tvořen dvěma ocelovými rošty, mezi nimiž bylo umístěno kamenivo. Testované přelivy měly šířku 10–30 cm a výšku 5–15 cm. Rozsah měřených průtoků byl od 0,2 l/s do 20 l/s.

Obr. 2. Umístění přelivu ve žlabu
Fig. 2. Measuring weir situated in the laboratory flume
Typický průběh pokusu lze charakterizovat následovně, ve žlabu je nainstalovaný příslušný měrný přeliv (není ovlivněn dolní vodou), na Thomsonově přelivu je nastaven požadovaný průtok a poloha hladiny před měrným přelivem se nemění (stav je ustálený). V této chvíli je možné odečíst polohu hladiny před měrným přelivem pomocí hrotových měřítek. První hrotové měřítko je umístěno ve skleněném válci spojeném dnovým odběrem se žlabem, dnový odběr se nachází 45 cm před měrným přelivem, tj. vzdálenost 3·hp,max protiproudně před měrným přelivem. Druhé hrotové měřítko měří výšku hladiny ve stejném místě a je umístěné na posuvném nosníku na vrcholu žlabu.
Průtoky do cca 7 l/s byly měřeny pomocí kalibrované měrné nádoby. Měrné nádoba měla tvar kvádru o rozměrech 0,4 m × 0,5 m × 0,3 m, hladina v nádobě byla měřena pomocí osazeného hrotového měřítka. Měrná nádoba byla opatřena koly, takže s ní bylo možné jednoduše a rychle manipulovat. Měření průtoku probíhalo následovně – pod přepadový paprsek pod měrným přelivem byla nasunuta měrná nádoba, v tento okamžik bylo započato měření času pomocí stopek, jakmile došlo k naplnění měrné nádoby, došlo k odsunutí měrné nádoby a zastavení stopek, tento postup byl obvykle dvakrát opakován pro každý pokus. Typická doba odběru byla 120–7 s. Nejistotu měření průtoku lze odhadnout pomocí uměle zavedené chyby měření času o velikosti 0,2 s. V mezním případě, kdy je průtok roven cca 7 l/s, je doba plnění měrné nádoby 7,1 s, pokud zavedeme umělou chybu ± 0,2 s, změní se hodnota měřeného průtoku o ± 3 %. Pro nízké průtoky s dlouhou dobou odběru je velikost chyby v řádech desetin procenta. Průtoky větší než 7 l/s byly měřeny pomocí kalibrovaného měrného Thomsonova přelivu umístěného před vtokem do žlabu. Lze předpokládat obdobnou přesnost měření průtoku jako pomocí měrné nádoby.
Ostrohranné měrné přelivy
V rámci laboratorního měření byly testovány tři ostrohranné přelivy pro měření malých průtoků (trojúhelníkový, obdélníkový a kruhový přeliv). Přelivná hrana testovaných přelivů byla konstruována následovně – šířka přelivné hrany byla 1 mm a poté byla zkosena pod úhlem 45° pro zajištění volného přepadového paprsku. Provedení přelivné hrany je ve shodě s normou ČSN ISO 1438 [1]. Testované geometrie přelivů a naměřené konsumční křivky jsou zobrazeny na obr. 3 a 4. Naměřené hodnoty byly konfrontovány s hodnoty predikovanými jednotlivými vzorci a dále bylo zkoumáno chování jednotlivých přelivů při minimálních přepadových výškách.
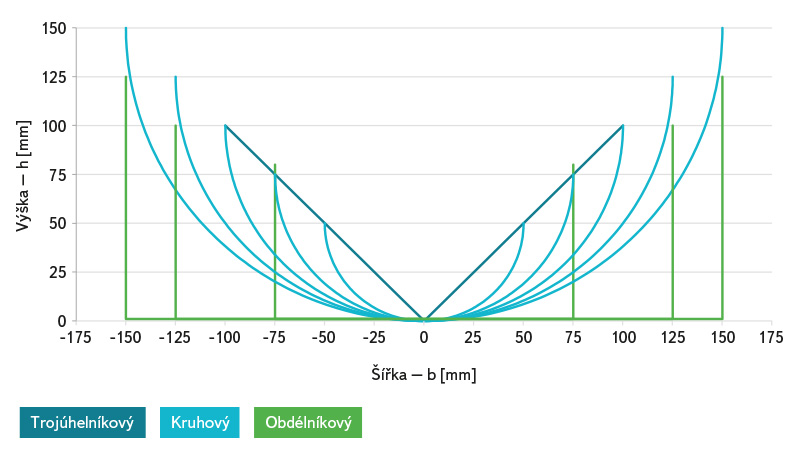
Obr. 3. Rozměry testovaných měrných přelivů
Fig. 3. Tested weir dimensions
Pro každý měrný přeliv byla určena hodnota přepadové výšky, pod kterou již dochází k „přilnutí“ přepadového paprsku na vlastní konstrukci měrného přelivu. Tato výška představuje limitní minimální výšku pro vlastní měření průtoku pomocí měrného přelivu. U obdélníkového přelivu dochází k přilnutí při výšce přepadového paprsku cca 10 mm, u trojúhelníkového přelivu při výšce cca 15 mm a u kruhového přelivu při výšce cca 20 mm.
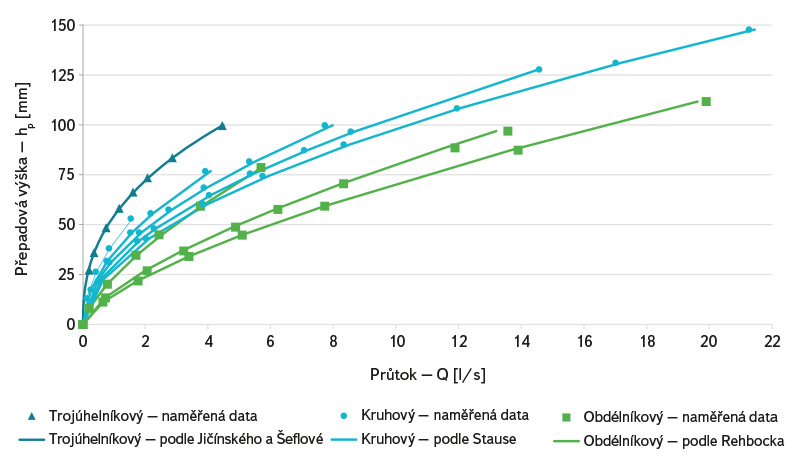
Obr. 4. Konsumční křivky ostrohranných přelivů z obr. 3 proložené vztahy vybraných autorů
Fig. 4. Sharp-crest weir discharge curves from fig. 3 with formulas from selected authors
Trojúhelníkový přeliv (Thomsonův)
Trojúhelníkový přeliv s vrcholovým úhlem o velikosti 90°, též nazýván „Thomsonův“ přeliv, je vhodný na lokality s velkým rozsahem měřených průtoků. Trojúhelníkový přeliv dokáže přesně měřit malé i velké průtoky, jeho nevýhodou je snadné zanesení průtočného profilu při minimálních přepadových výškách. Průtok trojúhelníkovým rovnoramenným přelivem lze obecně vypočítat následovně [2]:
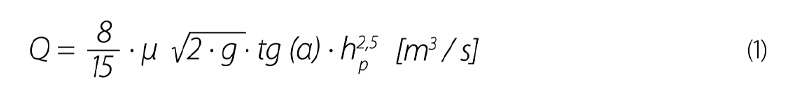
Pro trojúhelníkový pravoúhlý přeliv bývá nejčastěji udávána Thomsonova rovnice [3]:

Havlík [4] pro tento vztah udává meze platnosti 0,05 m < h < 0,18 m a zároveň B/h ≥ 8 a s/h ≥ 3.
Dále je také uváděna rovnice podle Kinga [5]:

Jičínský a Šeflová [2] navrhli na základě porovnání řady vztahů vztah pro výpočet:
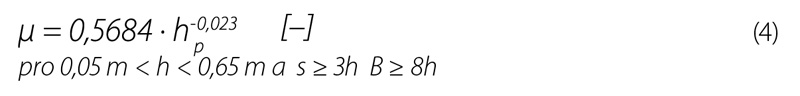
Porovnání výsledků měření na trojúhelníkovém přelivu s vrcholovým úhlem 90° s hodnotami stanovenými podle výše uvedených vzorců je zobrazeno na obr. 5. Porovnání je provedeno pomocí Rrel – relativního rozdílu měřeného průtoku a hodnotou průtoku stanoveného podle výše uvedených rovnic. Z porovnání je patrné, že největších relativních rozdílů je dosahováno při malých průtocích, resp. malých přepadových výškách. Při vyšších průtocích jsou již chyby zanedbatelné, neboť se již výška přepadového paprsku dostává do platných hodnot použitelnosti vzorců pro výpočet přepadového součinitele.
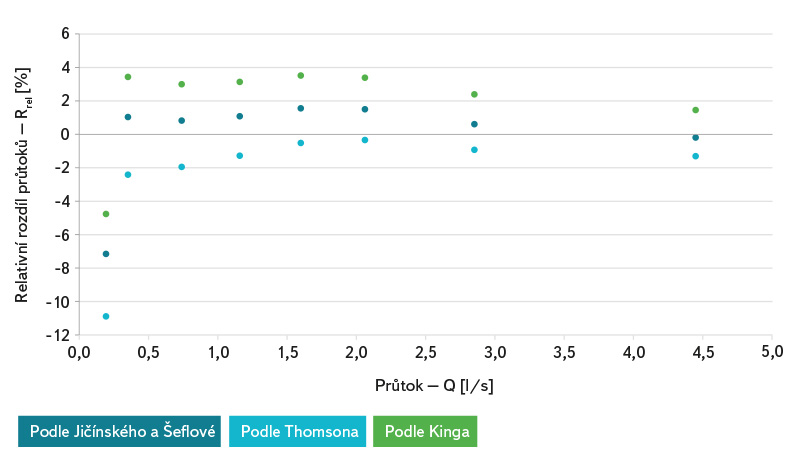
Obr. 5. Porovnání relativních rozdílů průtoků pro trojúhelníkový ostrohranný měrný přeliv
Fig. 5. Relative flow errors comparison of triangle sharp-crested weir
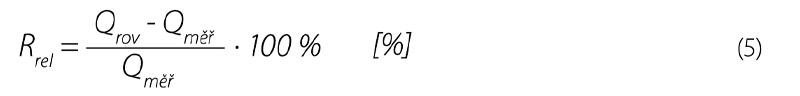
Porovnání naměřených součinitelů přepadu a hodnot součinitelů přepadu vypočtených z výše uvedených vztahů je zobrazeno na obr. 6. Pro trojúhelníkový přeliv a malé přepadové výšky se jeví jako optimální použití rovnice podle Jičínského a Šeflové (4) nebo podle Thomsona (2). Naopak podle měření nelze doporučit vztah podle Kinga (3).
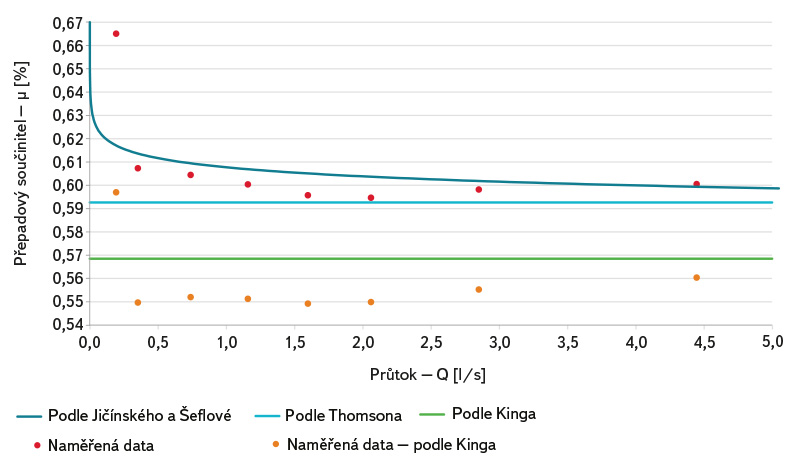
Obr. 6. Porovnání přepadových součinitelů pro trojúhelníkový přeliv
Fig. 6. Comparison of the overfall weir coefficients (triangle weir)
Obdélníkový přeliv
V rámci pokusů byly použity obdélníkové přelivy s kontrakcí, šířky přelivů byly 15–30 cm a výšky 8–12,5 cm. Obdélníkové přelivy lze s výhodou použít na vodní toky, jelikož mají dostatečnou kapacitu a nezpůsobí příliš velké vzdutí hladiny před měrným přelivem. Pro výpočet průtoku lez použít rovnici přepadu:
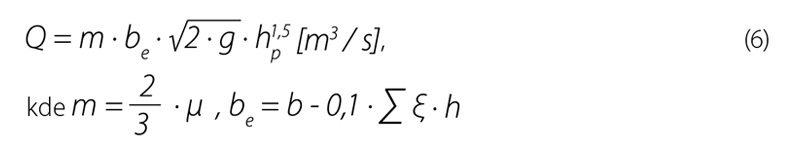
Porovnání výsledků měření na obdélníkových přelivech s hodnotami stanovenými podle výše uvedených vzorců je zobrazeno na obr. 7 a 8. Porovnání je provedeno pomocí Rrel (5). Z grafu je patrná poměrně dobrá shoda se vztahem podle Rehbocka (9), vztah podle Zschiedricha (8) naopak nelze doporučit. Často uváděný Héglyho vztah (7) dosahuje relativních rozdílů Rrel desítek až stovek procent a nelze ho pro nízké přepadové výšky doporučit. Porovnání naměřených součinitelů přepadu a hodnot součinitelů přepadu vypočtených z výše uvedených vztahů je zobrazeno na obr. 8. Z porovnání jsou patrné výše uvedené závěry o vhodnosti použití vztahů podle jednotlivých autorů.
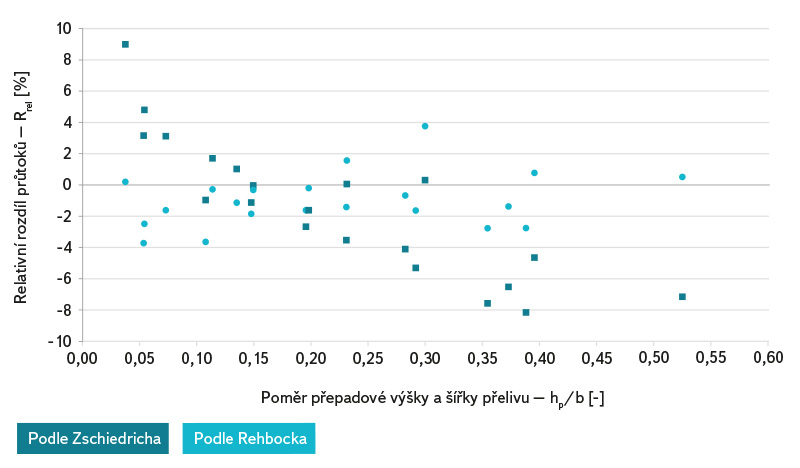
Obr. 7. Porovnání relativních rozdílů průtoků pro obdélníkový ostrohranný měrný přeliv
Fig. 7. Relative flow errors comparison of rectangular sharp-crested weir
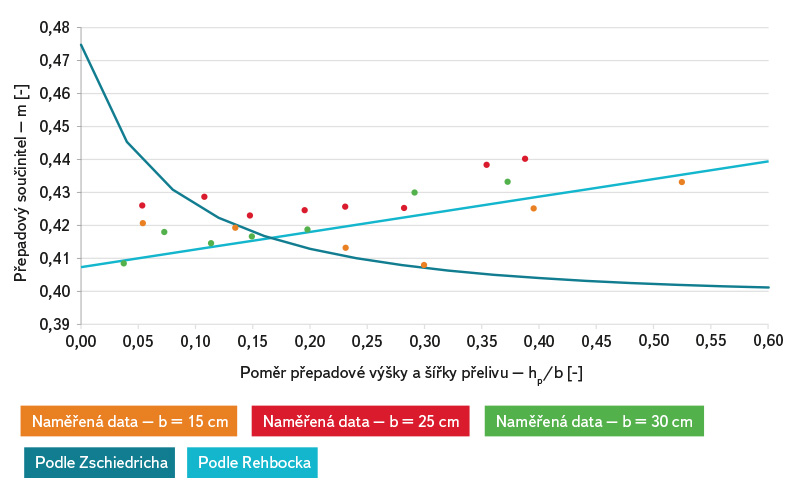
Obr. 8. Porovnání přepadových součinitelů pro obdélníkový přeliv
Fig. 8. Comparison of the overfall weir coefficients (rectangular weir)
Hodnota součinitele zúžení ξ byla uvažována 1. Součinitel přepadu m lze určit podle Héglyho vztahu [6]:
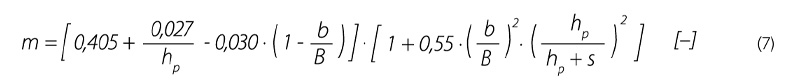
Součinitel přepadu lze dále určit například pomocí vztahu podle Zschiedricha [2]:
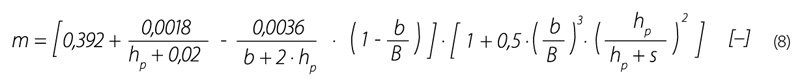
Případně lze určit přepadový součinitel μ podle Rehbocka [7]:
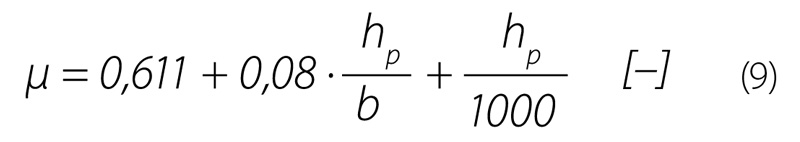
Kruhový přeliv
V rámci pokusů byly použity kruhové přelivy o poloměru 10 až 30 cm. Kruhové přelivy představují kompromis mezi trojúhelníkovým a obdélníkovým přelivem, dávají poměrně přesné hodnoty průtoku i při malých přepadových výškách a zároveň mají poměrně velkou maximální kapacitu v porovnání se stejně vysokým trojúhelníkovým přelivem. Pro výpočet průtoku kruhovým přelivem lze použít vztah odvozený Stausem [8]:
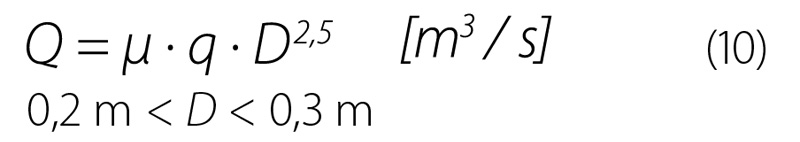
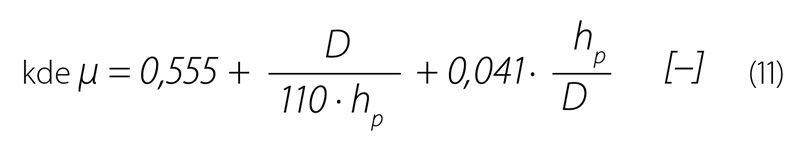
| kde | q | je | průtok při průměru kruhu 1 dm v závislosti na poměru hp/D. |
Porovnání výsledků měření na kruhových přelivech s hodnotami stanovenými podle výše uvedeného vzorce je zobrazeno na obr. 9 a 11. Na obr. 9 je zobrazeno porovnání relativních rozdílů průtoků Rrel (5) se vztahem podle Stause. Z grafu je patrné, že pro nízké hodnoty přepadových výšek je relativní rozdíl největší – cca 4 % a poté se plynule snižuje na cca 2 %. Porovnání naměřených přepadových součinitelů je zobrazeno na obr. 11, naměřené součinitele se liší od hodnot určených vztahem (11). Naměřená data byla proložena následující funkcí (byla vyřazena data, kdy byl průtok větší než 7 l/s, tj. stavy, kdy průtok nebyl měřen kalibrovanou nádobou):
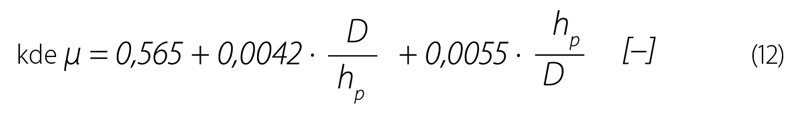
Vztah je ověřen pro přelivy o průměru 10 až 30 cm s ostrou hranou definovanou na začátku kapitoly a minimální přepadovou výškou 2 cm.
Na obr. 10 je zobrazen vliv uměle zanesené chyby při měření průtoku kalibrovanou měrnou nádobou definovanou výše v kapitole metodika experimentů. Pro přeliv o průměru 20 cm byly změněny doby plnění měrné nádoby o ± 0,2 s a následně byly určeny tomu odpovídající průtoky a přepadové součinitele.
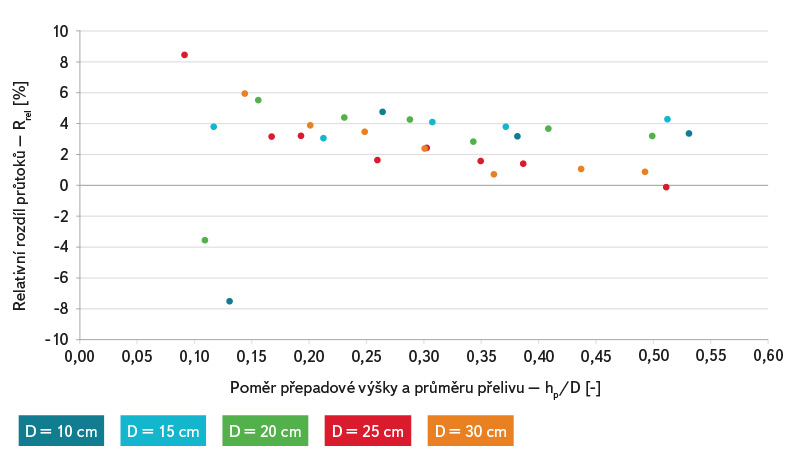
Obr. 9. Porovnání relativních rozdílů průtoků pro kruhový ostrohranný měrný přeliv
Fig. 9. Relative flow errors comparison of circular sharp-crested weir
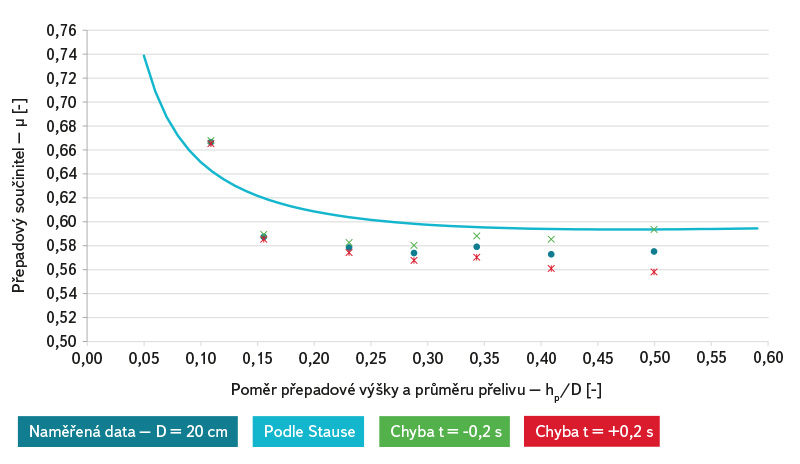
Obr. 10. Závislost hodnoty přepadového součinitele na přesnosti měření průtoku
Fig. 10. Dependency of the overfall weir coefficients on the flow measuring
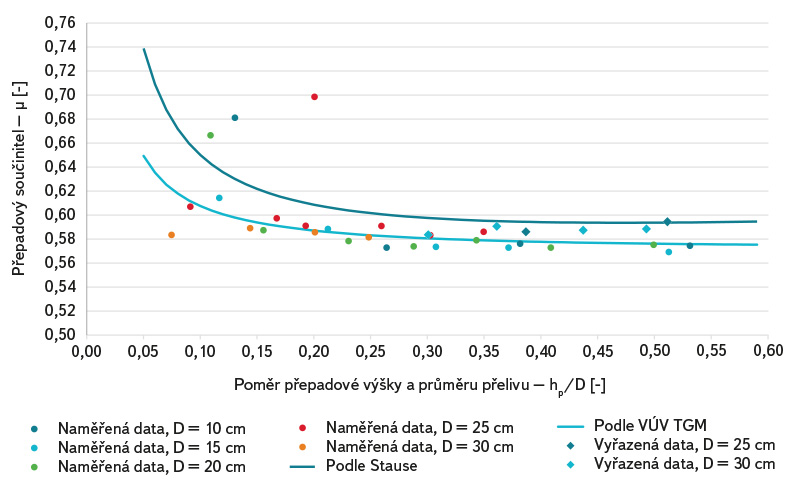
Obr. 11. Porovnání přepadových součinitelů pro kruhový přeliv
Fig. 11. Comparison of the overfall weir coefficients (circular weir)
Chyby při měření průtoků mohou zásadně ovlivňovat výsledky měření až při průtoku vyšším než cca 7 l/s, velikost této chyby byla redukována opakováním měření průtoku kalibrovanou nádobou.
Měrné přelivy s kruhovou přelivnou hranou
Velkým problémem, který nastává zejména v podzimních měsících, je ulpívání listů na přelivné hraně měrných přelivů. Polokruhová přelivná hrana je lépe, vůči ostré hraně, hydraulicky tvarovaná a listí by na ní nemuselo ulpívat v takové míře a zkreslovat naměřená data. V rámci výzkumu byly proto testovány měrné přelivy s kruhovou přelivnou hranou (obdélníkový (b = 15 cm a h = 8 cm) a kruhový (D = 20 cm)). Přelivná hrana byla tvořena půlkruhem o poloměru 2,5 mm, tj. tloušťka konstrukce přelivu byla celkem 5 mm, na vrcholu této konstrukce byla umístěna polokruhová přelivná hrana o poloměru 2,5 mm.
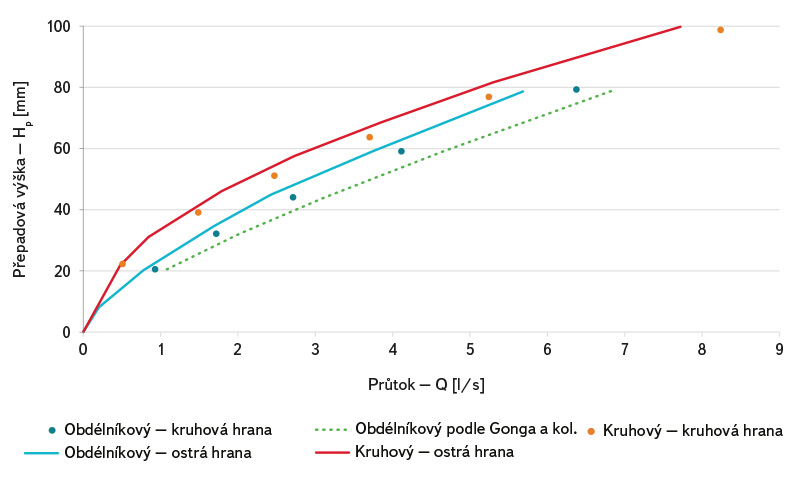
Obr. 12. Porovnání konsumčních křivek ostrohranné a kruhové přelivné hrany obdélníkového a kruhového přelivu
Fig. 12. Comparison of the sharp and semi-circle crest weir discharge curves (circle and rectangular weir)
Porovnání naměřených konsumčních křivek je zobrazeno na obr. 12. Z grafu je patrná větší kapacita měrného přelivu s polokruhovou hranou oproti ostré přelivné hraně. Zároveň je zde uveden vztah podle Gonga a kol. [9], kteří se zabývali měrnými obdélníkovými přelivy s polokruhovou přelivnou hranou. Gong a kol. prováděli měření na větších obdélníkových přelivech než jsou naše naměřená data, proto si nejspíše neodpovídají naměřená data s jejich odvozeným vztahem [9]:
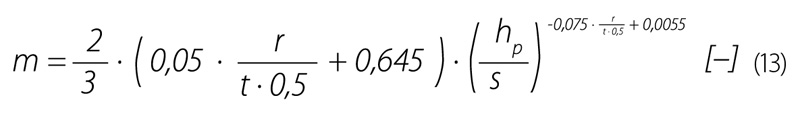
V rámci pokusů byly také určeny přepadové výšky, při nichž již dochází k přilnutí paprsku na konstrukci přelivu a jeho neodtržení od přelivné hrany. Pro obdélníkový přeliv je to cca 20 mm a pro kruhový přeliv cca 30 mm. Porovnání naměřených dat pro kruhovou hranu s ostrou přelivnou hranou pomocí relativních rozdílů velikosti průtoků je zobrazeno na obr. 13. Z grafu je patrné, že kruhová přelivná hrana je o cca 10 % kapacitnější než ostrá hrana. Porovnání je provedeno pomocí Rrel,KH:
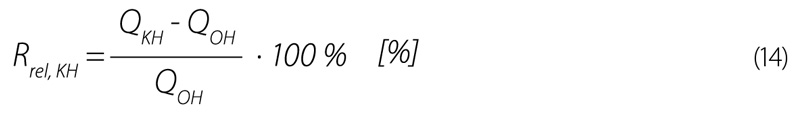
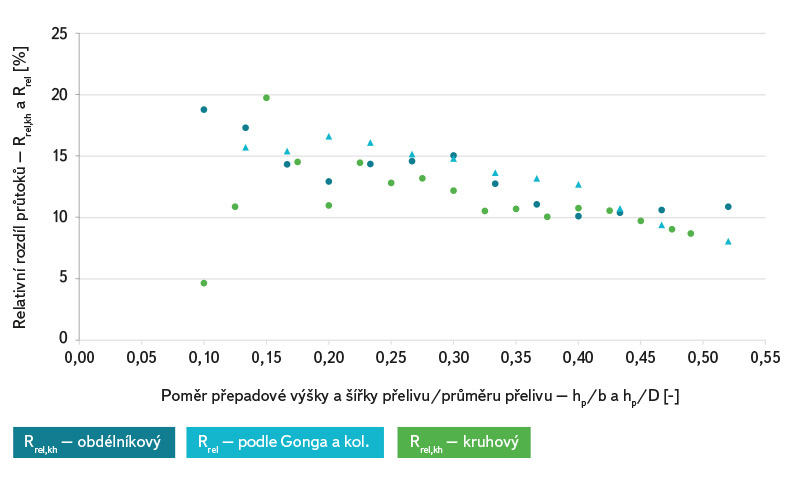
Obr. 13. Porovnání relativních rozdílů průtoku ostrohranných a kruhových hran měrných přelivů
Fig. 13. Comparison of the discharge´s relative differences of sharp and semi-circle crests weirs
Porovnání naměřených součinitelů přepadu pro kruhovou a ostrou přelivnou hranu je zobrazeno na obr. 14.
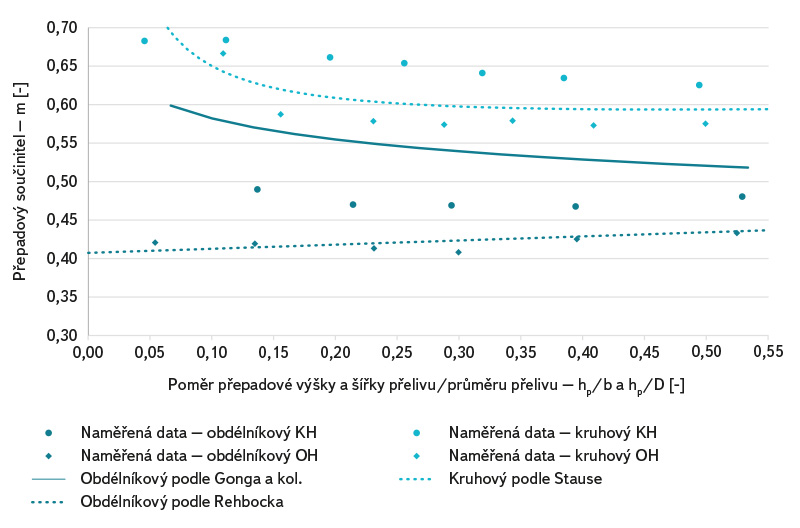
Obr. 14. Porovnání přepadových součinitelů pro kruhový a obdélníkový přeliv s ostrohrannou nebo kruhovou přelivnou hranou
Fig. 14. Comparison of the semi-circle and rectangular overfall weir coefficients with sharp and semi-circle crest
Umístění měrného přelivu vůči směru natékajícího proudu
V rámci pokusů prováděných ve žlabu byly také realizovány pokusy se záměrně „chybně“ umístěnými přelivy. Jako správně geometricky instalovaný přeliv lze definovat takový, který je svislý a půdorysně kolmý na osu koryta. Na vodním toku může dojít ke změně geometrie usazení přelivu například při vlastní chybné instalaci přelivu. Celkem byly testovány tři varianty změněného umístění přelivu (viz obr. 15) – vertikální náklon 1 a 2 (po a proti proudu, vlastní přeliv byl vůči svislému přelivu nakloněn o ± 10°) a horizontální náklon 3 (tj. přeliv nebyl kolmo vůči ose koryta, úhel mezi osou toku a přelivem byl 65°). Pokusy byly uskutečněny na obdélníkovém přelivu šířky 15 cm a výšky 8 cm. Výsledky této citlivostní analýzy jsou zobrazeny na obr. 16 pomocí relativní chyby Rrel,u, kde Qkolmý je roven průtoku přes geometricky správně usazený přeliv a Qupravený je rovný průtoku přes geometricky „chybně“ umístěný přeliv:

Z výsledků je patrné, že vertikální náklon po proudu způsobí chybu cca + 1,5 % vůči kolmé variantě při stejné přepadové výšce a obdobně je průtok o 2,5 % menší, pokud je přeliv o 10° nakloněn proti směru proudění. Půdorysné natočení přelivu vůči ose toku o 25° nezpůsobilo měřitelnou odchylku. Lze konstatovat, že chybné umístění přelivu, definované výše, nezpůsobí příliš velkou chybu měření. Toto tvrzení je ovšem ověřeno pouze pro malé měrné přelivy a nízké průtoky, v případě větších přítokových rychlostí lze očekávat zvětšení chyb měření průtoku.
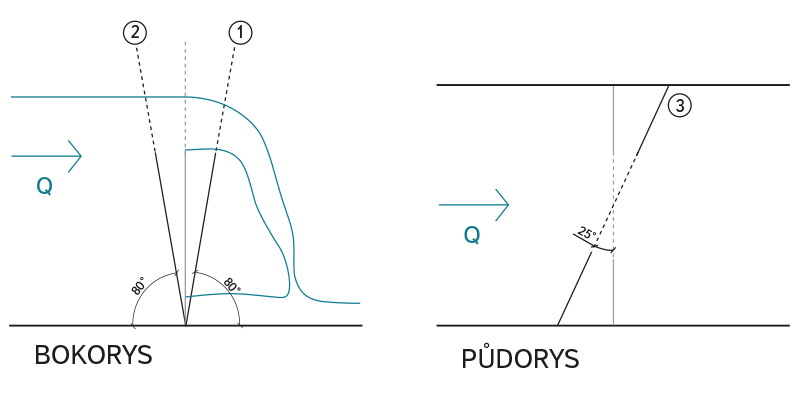
Obr. 15. Zobrazení změněných umístění přelivu vůči standardnímu umístění (šedá – standardní umístění, černá – změněné umístění)
Fig. 15. Different positions diagrams of the weir against the channel centre line (grey – standard position, black – different position)
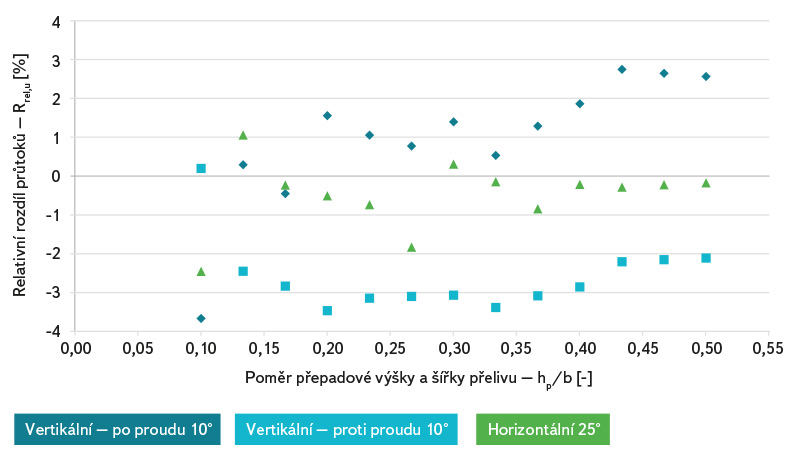
Obr. 16. Porovnání relativních chyb způsobených chybným geometrickým umístěním měrného přelivu v toku
Fig. 16. Relative errors comparison of different positions of the weir against the channel centre line
Výroba měrných přelivů
Měrné přelivy pro testování v laboratorním žlabu a v terénu byly zhotoveny metodou 3D tisku. Tato metoda umožňovala relativně snadné provedení variabilních tvarů měrného přelivu a přelivné hrany. Trojrozměrný model každého přelivu byl vytvořen na počítači a poté vytištěn tiskárnou. V rámci pokusů v laboratoři byl použit materiál PLA (kyselina polymléčná), tento materiál je plně biologicky odbouratelný, vyrábí se z kukuřičného škrobu. Jeho výhodou je snadný a rychlý tisk, nevýhodou je malá pružnost a křehkost materiálu, která ho vylučuje pro použití v terénu.
Pro využití v terénu se osvědčil materiál PET (polyethylentereftalát), který je známý díky plastovým lahvím. Materiál je dostatečně pevný a zároveň pružný a odolný proti vodnímu prostředí. V rámci terénního měření jsou již přelivy z PET instalovány dva roky, během tohoto období nebyly zjištěny žádné materiálové nedostatky, které by nepříznivě ovlivňovaly kvalitu měření průtoku. Velká výhoda materiálu v zimních měsících, při poklesu teploty několik stupňů pod nulu je, že nedochází k namrzání vody na vlastním přelivu v porovnání například s ocelovým přelivem.
Závěr
V rámci laboratorního měření byly testovány přelivy s ostrou přelivnou hranou – trojúhelníkový, obdélníkový a kruhový. Pro jednotlivé přelivy byly porovnány hodnoty naměřených přepadových součinitelů s hodnotami podle různých autorů při minimálních přepadových výškách. Pro trojúhelníkový přeliv s vrcholovým úhlem 90° se jeví jako optimální používat rovnici podle Jičínského a Šeflové (4) nebo podle Thomsona (2). Pro obdélníkový přeliv vychází nejlépe rovnice podle Rehbocka (9). Pro kruhový přeliv byl odvozen vztah podle VÚV TGM (12). Pro každý přeliv byla určena hodnota přepadové výšky, pod kterou dochází k přilnutí přepadového paprsku ke konstrukci přelivu a k hysterezi konsumční křivky (obdélníkový – 10 mm, trojúhelníkový – 15 mm, kruhový – 20 mm).
V rámci pokusů s polokruhovou přelivnou hranou byly naměřeny přepadové součinitele pro kruhový a obdélníkový přeliv. Pro kruhový a obdélníkový přeliv s polokruhovou přepadovou hranou byly určeny hodnoty přepadové výšky, pod kterou již dochází k ulpívání přepadového paprsku na přelivu – obdélníkový přeliv 20 mm a kruhový přeliv 30 mm. Polokruhová přepadová hrana nezaručuje při nízkých přepadových výškách dokonalé odtržení výtokového paprsku.
Soubor pokusů také obsahoval měření se záměrně chybně umístěnými přelivy vůči proudu. Výsledky měření ukázaly, že pokud je přeliv nakloněn o 25° v horizontální rovině, výsledky měření se neliší od kolmého umístění přelivu. Pokud je přeliv vertikálně nakloněn o 10° proti směru proudění, naměřené průtoky jsou o 2,5 % menší než v případě svislého umístění. Pokud je přeliv vertikálně nakloněn o 10° po směru proudění, měřené průtoky jsou o 1,5 % větší než v případě svislého umístění. Tyto závěry lze ale aplikovat pouze, pokud je rychlost proudění před měrným přelivem malá.
Poděkování
Příspěvek vznikl za podpory projektu Zéta I – TJ01000343 – Vývoj hydraulicky vhodného přelivu pro měření malých průtoků.
