Souhrn
V předložené studii byly testovány vybrané lineární a nelineární regresní modely, které popisují vzájemný vztah mezi parametry modelu Bilan, které jsou stanoveny na základě meteorologických a hydrologických řad a mezi retenčními charakteristikami stanovenými na základě vybraných geomorfologických charakteristik povodí.

Odvozené lineárně regresní modely umožňují odhad parametrů modelu Bilan na základě retenčních charakteristik, které odhadují retenci v ploše povodí S3, a charakteristik, které odhadují retenci v nivě povodí Smax, St a Dd. Uvedený příspěvek prezentuje první výsledky regionální analýzy zaměřené na kvantifikaci retenčních charakteristik analýzou geomorfologických charakteristik povodí.
Úvod
Retence vody v povodí je jedním z klíčových faktorů, které utvářejí výslednou hydrologickou bilanci povodí. Celkovou retenci vody pro dané povodí tvoří časově a prostorově proměnlivé zásoby vody zadržené ve sněhové pokrývce, na povrchu vegetačního pokryvu, na povrchu povodí, v nenasycené a nasycené zóně.
Jeden ze základních přístupů kvantifikace dynamiky celkové retence vody v povodí je založen na aplikaci matematického modelu hydrologické bilance, který umožňuje kontinuální simulaci hydrologické bilance pro vybraný řešený časový úsek. Celková retence je následně stanovena na základě podrobné analýzy simulovaných toků a zásob výsledné hydrologické bilance povodí. V podmínkách České republiky je pro potřeby řešení celé řady souvisejících inženýrských úloh využíván celistvý model hydrologické bilance Bilan [1, 2]. Model Bilan umožňuje popsat dynamiku jednotlivých zásob vody v povodí, která je vyjádřena jejich časovými řadami. K tomu účelu jsou používány vybrané časové řady meteorologických a hydrologických veličin.
Vedle simulací celkové retence kontinuálním modelem hydrologické bilance existuje celá řada empirických přístupů, které poskytují odhad retence vody v povodí. Jedním z nejrozšířenějších je empirický postup, který využívá čísla odtokových křivek (CN křivky) pro stanovení odhadu maximální retence povodí [3].
Dále celá řada studií poukazuje na vzájemný vztah mezi hydrologickým systémem povodí a geomorfologickými charakteristikami povodí [4–6]. Tyto vztahy je možné použít pro regionalizaci hodnot vybraných parametrů hydrologického modelu, která je založena na využití fyzikálních geomorfologických charakteristik povodí [4, 5]. V případě existence vzájemného vztahu mezi geomorfologickými charakteristikami povodí a parametry hydrologického modelu je možné kvantifikovat vliv nově navrhovaných retenčních opatření [7]. Podmínkou kvantifikace je existence vztahu mezi retenčními opatřeními a geomorfologickými charakteristikami [4].
Cílem předloženého příspěvku je popis vzájemného vztahu vybraných geomorfologických charakteristik povodí a vybraných parametrů hydrologického modelu Bilan, které nejvíce ovlivňují celkovou retenci vody v povodí. Na základě odvozených vztahů bude následně možné kvantifikovat vliv vybraných retenčních opatření v povodí na celkovou retenci vody v povodí.
Materiál a metody
Data povodí LAPV
V předložené studii byly použity dva druhy dat. První byl tvořen měsíčními meteorologickými a hydrologickými řadami pro povodí řešených v rámci Generelu lokalit pro akumulaci povrchových vod (LAPV). Druhý soubor dat je tvořen prostorovými daty, která umožňují stanovit vybrané charakteristiky povodí.
Pro každé povodí byla provedena kalibrace hydrologického modelu Bilan, jejímž výsledkem bylo stanovení hodnot parametrů modelu Bilan pro dané povodí LAPV. V předložené studii byly testovány parametry Spa a Grd.
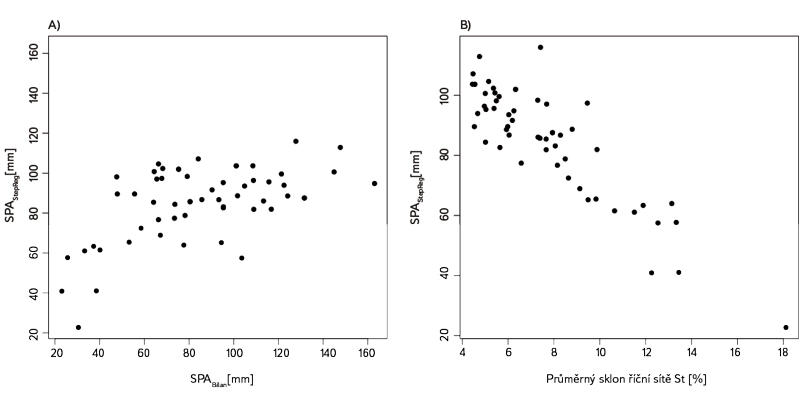
Obr. 1. Výsledky lineárního modelu krokové regrese pro parametr Spa; A) shoda mezi Spa stanoveným na základě kalibrace modelu Bilan a Spa stanoveným geomorfologickou analýzou; B) závislost Spa stanoveným geomorfologickou analýzou na průměrném sklonu říční sítě St
Fig. 1. Results of stepwise linear regression model for Spa parameter; A) scatter plot of Spa estimated using the Bilan model and Spa estimated using geomorphological analysis; B) relationship between Spa estimated using geomorphological analysis and average slope of river network
Parametr Spa vyjadřuje velikost nelineárního zásobníku zásoby půdní vody a intercepce v povodí v mm, který určuje část retence vody v povodí. Zvýšením hodnot Spa je zvýšena uvedená část celkové retence vody v povodí. Parametr Grd je součinitel zásobnosti akumulačních prostorů, které kontrolují základní odtok. Snížením hodnot Grd dochází ke zpomalení základního odtoku v povodí.
Analýza vzájemného vztahu geomorfologických charakteristik a parametrů modelu Bilan byla provedena na souboru vybraných 53 povodí LAPV. Na základě GIS analýz byly stanoveny pro každé povodí následující geomorfologické charakteristiky povodí: A – plocha povodí [km2]; CN1, CN2, CN3 – čísla odtokových křivek pro tři předchozí vláhové poměry; S1, S2, S3 – maximální retence povodí stanovená metodou CN pro tři typy předchozích vláhových poměrů [mm]; Dd – hustota říční sítě [km/km2]; L – celková délka říční sítě [km]; S – průměrný sklon říční sítě [%]; Sp – sklon povodí [%], Smax – maximální lokální sklon povodí [%].
Regresní modely
Pro stanovení vzájemného vztahu mezi vybranými parametry modelu Bilan (Spa a Grd) a geomorfologickými charakteristikami povodí (deskriptory) byly použity následující regresní modely: model vícerozměrné lineární regrese, model krokové regrese a nelineární regresní model založený na Gaussově procesu [8].
Vícerozměrný model lineární regrese určuje každý parametr modelu Bilan pomocí lineární kombinace hodnot vybraných geomorfologických charakteristik a neznámých parametrů, které byly stanoveny standardní metodou nejmenších čtverců [9].
Model krokové regrese pomocí iteračního výpočtu identifikuje vhodný soubor geomorfologických charakteristik, které vysvětlují testované parametry modelu Bilan. Pro potřeby řešení byl použit jednoduchý prunning algoritmus [10], který iterační výpočet začíná s modelem s největším počtem deskriptorů. V každé iteraci je následně postupně odebírán/přidáván deskriptor s nejmenším podílem na vysvětlení celkového rozptylu na základě výsledků F‑testu [9]. Iterační výpočet končí nalezením vhodného souboru statisticky významných deskriptorů. Pro výpočet modelem krokové regrese byly použity, v rámci každé iterace, modely vícerozměrné lineární regrese. Výsledný model krokové regrese je tedy vícerozměrný model lineární regrese, který předpovídá parametry modelu Bilan souborem statisticky významných deskriptorů geomorfologických charakteristik povodí.
Model nelineární regrese založený na Gaussově procesu je popsán funkcí střední hodnoty a kovarianční funkcí analyzovaného souboru dat. Pro vyjádření kovarianční funkce byly použity RBF funkce. Identifikace parametrů byla provedena metodou viz [11]. Pro stanovení hodnot parametrů Spa a Grd byly testovány soubory různých kombinací dvou a tří geomorfologických deskriptorů.
Celý výpočet byl proveden ve statistickém prostředí R, regresní modely Gaussova procesu byly počítány pomocí balíku kernlab [12].
Výsledky
Kalibrace modelu Bilan pro povodí LAPV
Pro kalibraci modelu Bilan byla využita data 53 povodí zpracovaných v rámci Generelu lokalit pro akumulaci povrchových vod (Generel LAPV). Pro stanovení hodnot parametrů Spa a Grd byl použit manuální a automatický kalibrační postup. Kvalita kalibrace byla ohodnocena na základě porovnání pozorovaných a vypočtených hodnot měsíčních výšek odtoku koeficientem determinace (NS) a hodnotami průměrné absolutní odchylky (MAE).
Hodnoty koeficientu determinace se nacházely v intervalu (0,03; 0,75). Průměrná hodnota NS byla rovna 0,48, medián 0,51, 50 % povodí bylo nakalibrováno s hodnotami NS mezi 0,38 a 0,59, u 25 % povodí byly výsledky kalibrace ohodnoceny hodnotou NS mezi 0,59 a 0,75.
Hodnoty průměrné absolutní odchylky se nacházely v intervalu (1,91; 13,68). Průměrná hodnota MAE byla rovna 7,64 mm, medián 6,73 mm, 50 % povodí bylo nakalibrováno s hodnotami MAE mezi 5,50 mm a 9,83 mm, u 25 % povodí byly výsledky kalibrace ohodnoceny hodnotou MAE mezi 1,91 mm a 5,50 mm.
Identifikované hodnoty parametru Spa se pohybovaly v rozpětí 23 mm a 163 mm, průměrná hodnota Spa byla rovna 84,13 mm, medián 80,43 mm, 50 % povodí mělo hodnotu Spa mezi 64,39 mm a 108,60 mm, u 25 % povodí byla celková retence půdního a intercepčního zásobníku mezi 108,60 mm a 163 mm, pro 25 % povodí s nejnižší hodnotou Spa byla hodnota parametru nalezena mezi 23 mm až 64 mm.
Identifikované hodnoty parametru Grd se nacházely v rozpětí 0,05 a 0,50 mm, průměrná hodnota Grd byla rovna 0,52, medián 0,25, 50 % povodí mělo hodnotu Grd mezi 0,20 a 0,31, u 25 % povodí byla hodnota součinitele zásobnosti pro zásobník podzemní vody mezi 0,31 a 0,50, pro 25 % povodí s nejnižší hodnotou Grd byla hodnota parametru nalezena mezi 0,05 až 0,20.
Kroková regrese
Pro stanovení parametru Spa byl identifikován následující lineární model na základě krokové regrese:
Spa = 0,71 S3 + 88,91 Dd – 8,89 St + 65,76 (1)
kde hlavní soubor deskriptorů je tvořen S3 maximální retencí pro III. typ předchozích vláhových podmínek [mm]; Dd je hustota říční sítě povodí [km/km2] a St průměrný sklon říční sítě v [%]. Celý soubor představuje statisticky významné vstupní veličiny, což bylo potvrzeno výsledky F testu a t‑testů, koeficient determinace lineárního modelu je roven 0,33. Výslednou závislost ukazuje obr. 1 a. Nejtěsnější lineární shodu mezi hodnotami Spa a použitými deskriptory vykazuje vztah mezi sklonem toku a Spa (viz obr. 1 b).
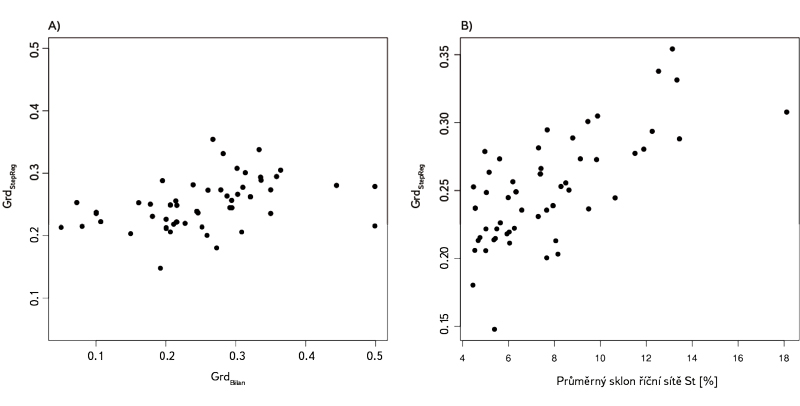
Obr. 2. Výsledky lineárního modelu krokové regrese pro parametr Grd; A) shoda mezi Grd stanoveným na základě kalibrace modelu Bilan a Grd stanoveným geomorfologickou analýzou; B) závislost Grd stanoveným geomorfologickou analýzou na průměrném sklonu říční sítě St
Fig. 2. Results of stepwise linear regression model for Grd parameter; A) scatter plot of Grd estimated using the Bilan model and Grd estimated using geomorphological analysis; B) relationship between Grd estimated using geomorphological analysis and average slope of river network
Pro parametr Grd byl krokovou regresí stanoven následující lineární model:
Grd = 0,02 St – 0,003 Smax + 0,23 (2)
kde soubor deskriptorů je tvořen St průměrným sklonem říční sítě v [%], Smax maximálním lokálním sklonem v povodí v [%]. Opět výsledný model obsahuje statisticky významné vysvětlující geomorfologické veličiny podle F testu a t‑testů, koeficient determinace je roven 0,17 (viz obr. 2 a). Nejtěsnější shodu deskriptorů a hodnot Grd opět vykazoval vztah mezi Grd a sklonem říčního systému St (viz obr. 2 b).
Jak je patrné ze závislostí na obr. 1 b a 2 b při implementaci revitalizačních opatření, které vedou ke snížení podélného sklonu toků v povodí, bude zvýšena celková retence v povodí. Rovnice 1 a 2 umožňují kvantifikovat retenci pomocí odhadu hodnot parametrů Spa a Grd a následném využití při simulaci hydrologické bilance modelem Bilan.
Nelineární regrese – Gaussovský proces
Na základě testování různých nelineárních regresních modelů byly pro oba parametry vybrány následující modely. Parametr Spa byl odhadován pomocí St průměrného sklonu říční sítě v [%] a hodnot odtokových křivek CN2 pro druhý typ předchozích vláhových poměrů. Parametr Grd byl odhadován na základě celkové délky říční sítě v povodí Lt [km] a hodnot odtokových křivek CN3 pro třetí typ předchozích vláhových poměrů.
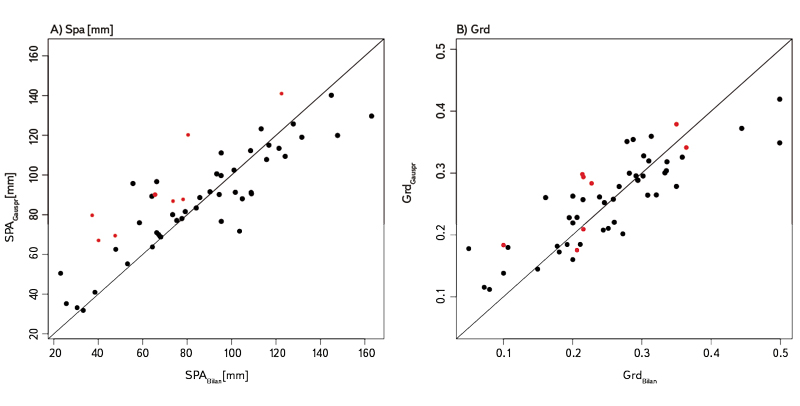
Obr. 3. Kalibrace a validace nelineárního regresního modelu, černě jsou znázorněny výsledky kalibrace, červeně jsou zobrazeny výsledky validace
Fig. 3. Calibration and validation results of nonlinear regression model, black dots show the calibration dataset and the red dots show the validation dataset
Validační postup nelineárních regresních modelů, založených na Gaussovském procesu, se skládal z kalibrace regresních modelů na kalibračních souborech dat, validace byla provedena pro osm náhodně vybraných povodí, která nebyla zahrnuta do kalibračního souboru. Validační výsledky modelů obou parametrů ukazují grafy na obr. 3.
Kvalita kalibrace regresního modelu pro Spa byla kvantifikována lineárním modelem mezi hodnotami parametru SpaBILAN stanovenými na základě meteorologických a hydrologických časových řad a hodnotami SpaGAUSSPR stanovenými na základě geomorfologických charakteristik. Koeficient determinace pro kalibrační soubor byl roven 0,81, pro validační soubor 0,82. MAE byla rovna 11 mm pro kalibrační soubor a 25 mm pro validační soubor.
Kvalita regresního modelu pro parametr Grd byla opět ohodnocena lineárním regresním modelem mezi GrdBILAN stanoveným na základě meteorologických a hydrologických časových řad a hodnotami GrdGAUSSPR stanovenými na základě geomorfologických charakteristik. Koeficient determinace pro kalibrační soubor byl roven 0,74, pro validační soubor 0,72. MAE byla rovna 0,04 pro kalibrační soubor a 0,05 pro validační soubor.
Výsledný vztah mezi parametry odvozenými na základě použitých geomorfologických charakteristik ukazuje obr. 4.
Diskuse
Podle výsledků kalibrace byl úspěšnější nelineární regresní model než lineární regresní model. Při hledání vhodného nelineární regresního modelu byly zkoušeny různé soubory deskriptorů. Uvedené modely byly úspěšnější než zmíněné lineární modely. Podobné výsledky byly dosaženy v práci [5].
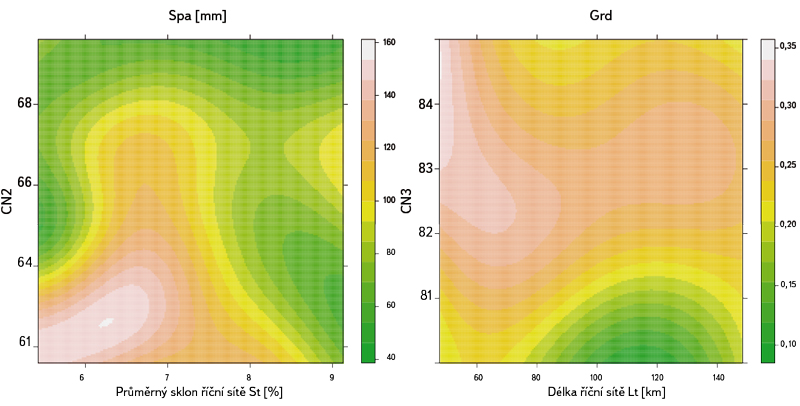
Obr. 4. Vztah mezi Spa, průměrným sklonem říční sítě a CN2 číslem odtokových křivek (levá část obrázku); vztah mezi Grd délkou říční sítě a číslem odtokových křivek CN3 (pravá část obrázku)
Fig. 4. The relationship between Spa and average slope of river network St and curve number CN2 (left part of the figure); the relationship between Grd and length of river network and curve number CN3 (right part of the figure)
Skladba deskriptorů a odvozené vztahy jsou logické, např. zvýšení zásob podzemní vody může být dosaženo revitalizačním opatřením, jehož záměrem je zvětšení celkové délky toků, v rámci nichž je předpokládáno zvýšení infiltrace v nivním systému. Odvozený regresní model pro parametr Grd umožňuje rámcově kvantifikovat vliv tohoto opatření na hydrologický systém povodí. Podobně při snížení hodnoty CN změnou land use a zpomalením odtoku souborem revitalizačních opatření, které snižují průměrný sklon říční sítě, dojde ke zvýšení retence v povodí, která je charakterizována hodnotou parametru Spa. Odvozené regresní vztahy je možné alternativně stanovit souhrnnou regionální kalibrací modelu Bilan podle postupu [7].
Závěr
V předložené studii je navržen metodický postup, který dále umožňuje rámcově kvantifikovat vliv přírodě blízkých retenčních opatření na hydrologický systém povodí. Navržený postup umožňuje stanovit hodnoty parametrů modelu Bilan pro povodí, jehož hydrologický systém je ovlivněn plošnými a liniovými přírodě blízkými retenčními opatřeními. Na výsledky studie bude navazovat posouzení vlivu souboru retenčních opatření kontinuální simulací hydrologické bilance modelem Bilan v povodích LAPV.
Poděkování
Tento článek vznikl v rámci řešení projektu Možnosti kompenzace negativních dopadů klimatické změny na zásobování vodou a ekosystémy využitím lokalit vhodných pro akumulaci povrchových vod (TA04020501), který je spolufinancován Technologickou agenturou České republiky.
