Korekce chyb srážek a teploty z regionálních klimatických modelů – vliv na modelování odtoku

Souhrn

Pro odhad vlivu změny klimatu na vodní režim v krajině a sektory vodního hospodářství se zpravidla užívá hydrologického modelování, kde vstupem do hydrologického modelu jsou scénářové srážky a teploty založené na simulacích klimatických modelů. Tyto simulace jsou zatíženy systematickými chybami, které lze korigovat pomocí řady dostupných metod. Nicméně se ukazuje, že shoda rozdělení korigovaných a pozorovaných vstupních veličin (srážek a teploty) nezaručuje shodu rozdělení simulovaného odtoku. To je způsobeno zejména skutečností, že běžně používané metody korekce systematických chyb klimatických modelů neodstraňují chyby v časové struktuře srážek. Dalším problémem je, že korekce se zpravidla omezují na časové měřítko, v němž je (hydrologický) model provozován – tj. většinou denní. Ukazuje se, že přes uspokojivou korekci veličin v denním časovém kroku jsou měsíční, sezonní a roční agregace srážek zatíženy podstatnou systematickou chybou, což následně vede k chybám v dlouhodobé hydrologické bilanci a variabilitě simulovaného odtoku.

Úvod

Jelikož jsou simulace klimatických modelů zatíženy systematickými chybami, nelze simulované časové řady srážek a teploty použít přímo pro hydrologické modelování. Relativně hrubé horizontální rozlišení globálních i regionálních klimatických modelů (RCM) neumožňuje adekvátně popsat orografii terénu, vznik konvektivních srážek atp. V důsledku toho je řada jevů popsána pomocí empirických nebo semi­‑empirických vztahů, které jsou často zmiňovány jako jedna z dominantních příčin systematických chyb v simulacích klimatických modelů [1–3].

Existuje řada studií, které se zabývají korekcí chyb klimatických modelů. Korekce simulovaných srážek a teploty spočívá v transformaci simulovaných časových řad takovým způsobem, který zaručí přijatelnou shodu vybraných statistických charakteristik simulovaných a pozorovaných veličin. Byly vyvinuty různé metody korekce systematických chyb, od transformací korigujících průměr přes nelineární transformace korigující průměr a variabilitu až po pokročilé metody transformující celé rozdělení pravděpodobnosti uvažovaných veličin, popř. vztahy mezi proměnnými. Tyto metody představuje např. [4–6]. Řada aspektů korekce systematických chyb je však problematická, viz např. [7, 8].

Simulace RCM jsou zpravidla k dispozici v denním časovém kroku. V tomto časovém měřítku také probíhá korekce simulovaných veličin i hodnocení její účinnosti. Současné metody korekce systematických chyb jsou schopné transformovat simulovaná data tak, že rozdělení korigovaných veličin se perfektně shoduje s rozdělením veličin pozorovaných a navíc rozumně zachovává korelační strukturu mezi veličinami. Shoda rozdělení a vztahů veličin v denním kroku však neznamená shodu v případě delších či kratších časových měřítek, což je způsobeno časovou strukturou simulovaných veličin, která není zpravidla korekcí ovlivněna. Toto chování bylo popsáno např. v pracích Haerter aj. [9], Johnson a Sharma [10], Ehret aj. [7] a Addor aj. [8], nicméně ve většině praktických aplikací je tento problém často přehlížen. Hodnocení metod korekce se navíc často omezuje na veličiny simulované klimatickým modelem (např. srážky a teplota) a neuvažuje výstupy závislé na těchto veličinách (např. odtok).

V předkládaném článku jsou proto demonstrovány základní problémy korekce systematických chyb při použití v hydrologických simulacích. Ukazuje se, že rozdělení odtoku simulovaného pomocí hydrologického modelu využívajícího korigované srážky a teplotu neodpovídá rozdělení odtoku simulovaného na základě pozorovaných časových řad ani v časovém kroku, ve kterém byla korekce provedena. Pro analýzu účinnosti metod korekce systematických chyb na různé veličiny v různých časových měřítcích byl vyvinut balík MUSICA pro R software, viz https://github.com/hanel/musica.

Popis oblasti a data

Studie byla provedena na povodí Oslavy, které má rozlohu 861 km² s průměrnou výškou 500 m n. m. Průměrná roční srážka činí 594 mm, průměrná teplota 7,2 °C a průměrný průtok v ústí je 3,5 m³/s. Povodí je z větší části neregulované, pouze na horním toku Oslavy je víceúčelová vodárenská nádrž Mostiště. Nevyskytují se zde vyšší elevace, které by znesnadňovaly použití RCM.

Pozorovaná data

Pro studii byla použita hydrometeorologická data (srážky, teplota, průtoky) v denním kroku z období 1970–1999. Časové řady srážek a teploty pocházejí z interpolovaných dat do pravidelné sítě 25 × 25 km [11], průtoky pak z vodoměrné stanice Oslavany.

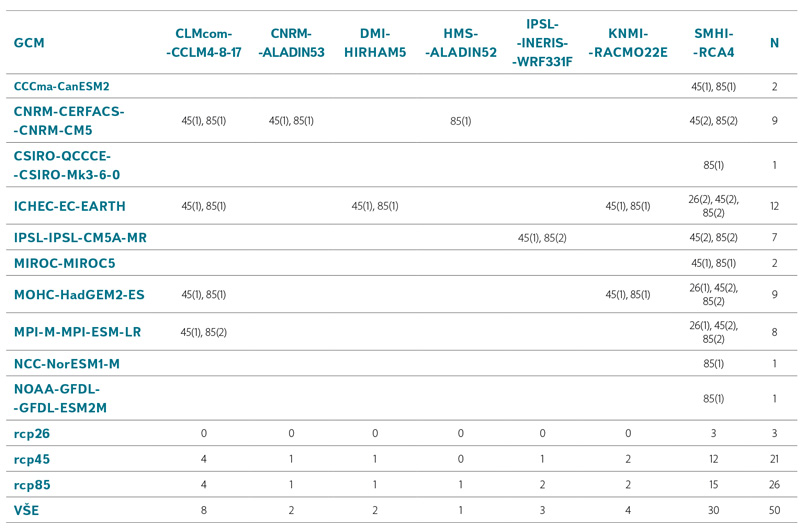
Tabulka 1. Použité RCM simulace; v řádcích jsou uvedeny řídicí simulace globálních klimatických modelů, sloupce odpovídají regionálním klimatickým modelům; v jednotlivých buňkách je v závorkách uveden počet simulací podle RCP2.6 („26“), RCP4.5 („45“) a RCP8.5 („85“)
Table 1. Considered RCM simulations; driving GCM simulations are listed in rows whereas columns correspond to RCMs; a number of simulation according to RCP2.6 („26“),
RCP4.5 („45“) and RCP8.5 („85“) is listed in brackets in individual cells

RCM data

Pro vyhodnocení účinku korekce systematických chyb simulovaných časových řad srážek a teploty na simulovaný odtok bylo uvažováno 52 simulací regionálních klimatických modelů z projektu CORDEX [12]. Přehled použitých simulací udává tabulka 1. K dispozici bylo sedm regionálních klimatických modelů k downscalingu simulací deseti globálních klimatických modelů. Z regionálních klimatických modelů je nejpočetněji zastoupen model RCA4 (30 simulací) a CLM (8 simulací). Simulace nejčastěji využívají koncentrační scénář RCP8.5 předpokládající nejintenzivnější zvyšování radiačního působení (26 simulací) a RCP4.5 (21 simulací), méně pak RCP2.6 předpokládající snižování koncentrací skleníkových plynů (3 simulace). Pro RCP6.0 nebyla dostupná žádná simulace. Simulace jsou většinou dostupné pro období cca 1961–2100, některé 1950–2100. Prostorové rozlišení je 0,11° a 0,44°, což odpovídá cca 12 a 50 km. Všechny simulace jsou volně dostupné prostřednictvím Earth System Grid Federation.

Metodika

Pozorované časové řady srážek a teploty byly použity pro kalibraci hydrologického modelu Bilan (kap. Hydrologické modelování). Simulované časové řady srážek a teploty byly korigovány standardní a kaskádovou kvantilovou metodou (kap. Korekce systematických chyb). Vybrané charakteristiky rozdělení korigovaných srážek, teploty a odpovídajícího modelovaného odtoku byly porovnány (kap. Vyhodnocení) s charakteristikami pozorovaných veličin (srážek, teploty a odpovídajícího modelovaného odtoku).

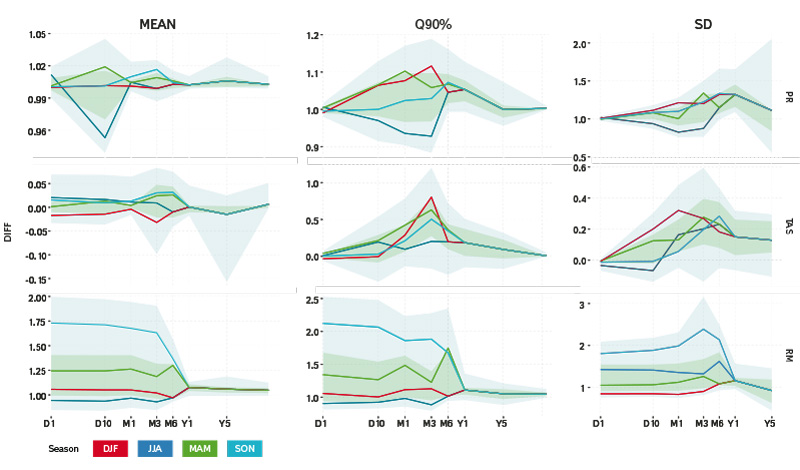
Obr. 1. Zbytková chyba (relativní pro srážky a odtok, absolutní pro teplotu [°C]) po korekci standardní kvantilovou metodou pro průměr (vlevo), 90% kvantil (uprostřed) a směrodatnou odchylku (vpravo), pro srážky (nahoře), teplotu (uprostřed) a modelovaný odtok (dole); barvy určují roční období (červená – zima, zelená – jaro, modrá – léto, světle modrá – podzim); vodorovná osa značí časové agregace (D1 – den, D10 – deset dnů, M1 – měsíc, M3 – tři měsíce, M6 – šest měsíců, Y1 – rok, Y5 – pět let); čáry značí průměrnou chybu, zelený pás rozpětí 50 % a modrý pás 90 % ze všech modelů
Fig. 1. Residual error (relative for precipitation and runoff, absolute for temperature [°C]) after the standard quantile correction method for mean (left), 90% quantile (middle) and standard deviation (right), for precipitation (top), temperature (middle) and simulated runoff (bottom); colours indicate seasons (red – winter, green – spring, blue – summer, light blue – autumn); horizontal axis shows time aggregation (D1 – a day, D10 – ten days, M1 – a month, M3 – three months, M6 – six months, Y1 – a year, Y5 – five years); the lines represent mean residual error in the climate model ensemble, green (blue) area indicates an envelope of 50 (90)% of climate model simulations

Korekce systematických chyb

Simulované časové řady srážek a teploty byly korigovány pomocí standardní kvantilové metody popsané např. [13]. Tato metoda zaručuje, že rozdělení pravděpodobnosti srážek a teploty korigovaných dat odpovídá rozdělení pravděpodobnosti pozorovaných veličin. Kvantilová metoda byla použita v denním kroku, zvlášť pro jednotlivé měsíce.

Za účelem vyhodnocení vlivu korigovaného časového měřítka na modelovaný průtok byla kvantilová metoda aplikována také iterativně pro různá časová měřítka (konkrétně denní, měsíční a roční) pomocí přístupu popsaného Haerterem aj. [9]. Podstatou metody je opakovaná korekce denních časových řad na základě rozdělení denních hodnot a měsíčních a ročních agregací. Vzhledem k tomu, že korekce v jednom časovém měřítku ovlivňuje rozdělení v jiných časových měřítcích, je postup iterativně opakován.

Hydrologické modelování

Simulace odtoku z povodí Oslavy byla provedena modelem Bilan vyvíjeným ve Výzkumném ústavu vodohospodářském (VÚV). Bilan [14] je konceptuální model hydrologické bilance, který je v denním kroku řízen šesti parametry. Srážky jsou transformovány na odtok pomocí soustavy lineárních a nelineárních nádrží. Kalibrace parametrů modelu probíhá na pozorovaných časových řadách (srážky, teplota a odtok), kdy se sleduje nejlepší shoda mezi pozorovaným a modelovaným odtokem. Nakalibrovaným modelem se dále generuje odtok na základě korigovaných srážek a teploty vycházejících z RCM. Více o modelu lze nalézt na bilan.vuv.cz.

Vyhodnocení

K vyhodnocení zbytkové chyby v korigovaných časových řadách srážek, teploty a modelovaného odtoku byl použit balík MUSICA pro prostředí R [15]. Balík umožňuje pohodlné porovnání libovolných charakteristik rozdělení hodnocených veličin pro různá časová měřítka, přičemž tato měřítka je možno uživatelsky definovat. V tomto článku jsou dále uvažována denní (D1), 10denní (D10), měsíční (M1), 3 a 6měsíční (M3 a M6) a roční a pětileté (Y1 a Y5) časové agregace. Pro kratší než půlroční agregace jsou výsledky prezentovány jako průměry pro jednotlivé sezony (MAM – březen, duben, květen; JJA – červen, červenec, srpen; SON – září, říjen, listopad; DJF – prosinec, leden, únor). Primárně se hodnotí chyba korigovaných veličin, která je dále označována jako „zbytková chyba“.

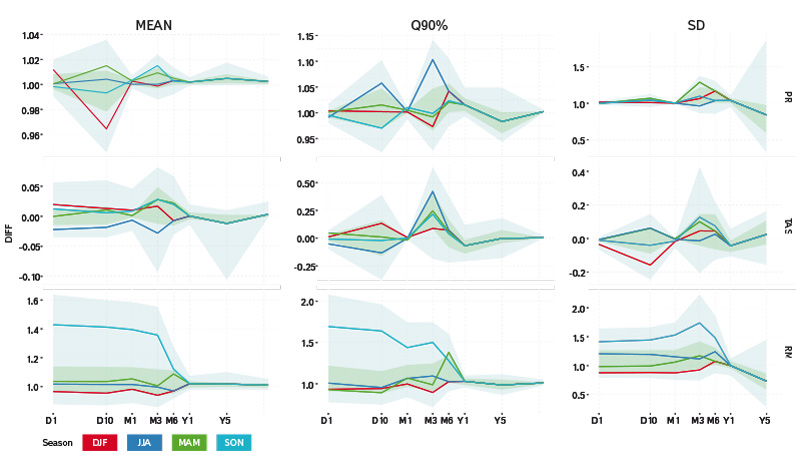
Obr. 2. Zbytková chyba (relativní pro srážky a odtok, absolutní pro teplotu [°C]) po korekci kaskádovou kvantilovou metodou pro průměr (vlevo), 90% kvantil (uprostřed) a směrodatnou odchylku (vpravo), pro srážky (nahoře), teplotu (uprostřed) a modelovaný odtok (dole); barvy určují roční období (červená – zima, zelená – jaro, modrá – léto, světle modrá – podzim); vodorovná osa značí časové agregace (D1 – den, D10 – deset dnů, M1 – měsíc, M3 – tři měsíce, M6 – šest měsíců, Y1 – rok, Y5 – pět let); čáry značí průměrnou chybu, zelený pás rozpětí 50 % a modrý pás 90 % ze všech modelů
Fig. 2. Residual error (relative for precipitation and runoff, absolute for temperature [°C]) after the cascade quantile correction method for mean (left), 90% quantile (middle) and standard deviation (right), for precipitation (top), temperature (middle) and simulated runoff (bottom); colours indicate seasons (red – winter, green – spring, blue – summer, light blue – autumn); horizontal axis shows time aggregation (D1 – a day, D10 – ten days, M1 – a month, M3 – three months, M6 – six months, Y1 – a year, Y5 – five years); the lines represent mean residual error in the climate model ensemble, green (blue) area indicates an envelope of 50 (90)% of climate model simulations

Výsledky

Z obr. 1 a 2 je patrné, že pro všechny tři prezentované charakteristiky (průměr, 90% kvantil a směrodatná odchylka) jsou zbytkové chyby velmi malé u srážek i teploty, zejména v D1 měřítku, pro které byly korekce kalibrovány. Nicméně v případě použití těchto srážek a teplot pro modelování odtoku dochází k „zesílení“ zbytkových chyb nad únosnou mez. Uspokojivé výsledky se nedostavily ani pro měřítko D1, pro které byly korekce kalibrovány. Extrémním případem je podzimní sezona (světle modře) – v absolutním vyjádření se však jedná o velmi malé hodnoty.

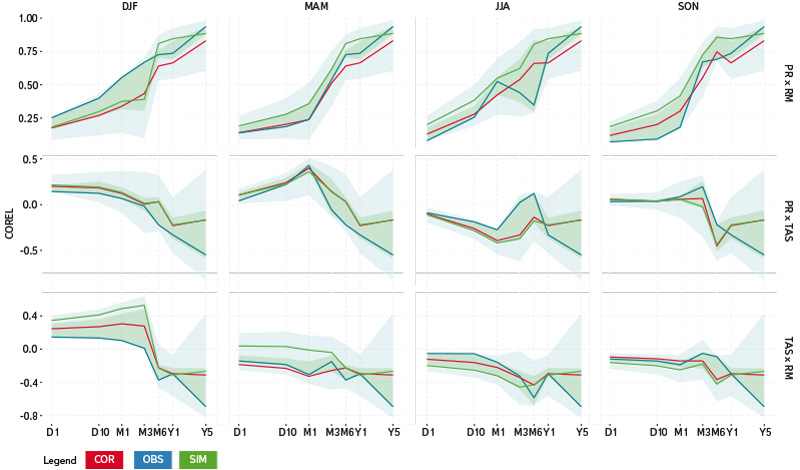
Obr. 3. Korelace mezi srážkou a modelovaným odtokem (nahoře), mezi srážkou a teplotou (uprostřed) a mezi teplotou a modelovaným odtokem (dole) pro jednotlivá roční období (DJF – zima, MAM – jaro, JJA – léto, SON – podzim); červeně jsou zobrazena korigovaná data standardní kvantilovou metodou, modře pozorovaná data a zeleně simulovaná data; vodorovná osa značí časová měřítka (D1 – den, D10 – deset dnů, M1 – měsíc, M3 – tři měsíce, M6 – šest měsíců, Y1 – rok, Y5 – pět let); čáry značí průměrnou korelaci, zelený pás rozpětí 50 % a modrý pás 90 % ze všech modelů
Fig. 3. Correlation between precipitation and modelled runoff (above), between precipitation and temperature (middle) and between temperature and modelled runoff (below) for seasons of year (DJF – winter, MAM – spring, JJA – summer, SON – autumn); data corrected by the standard quantile method are in red, observed in blue and simulated in green; horizontal axis shows time aggregation (D1 – a day, D10 – ten days, M1 – a month, M3 – three months, M6 – six months, Y1 – a year, Y5 – five years); the lines represent mean correlation coefficient, green (blue) area indicates an envelope of 50 (90)% of climate model simulations

Korekce kaskádovou kvantilovou metodou (obr. 2) přináší výrazně lepší výsledky. Je vidět, že rozpětí chyb u srážek a teploty je v měřítcích M1 a Y1 podstatně nižší než v případě korekce standardní kvantilovou metodou (obr. 1). Bohužel u agregací D10, M3 a M6 se již tak výrazné zlepšení nevyskytuje, jelikož tyto nebyly zahrnuty do kaskádové korekce. Je zajímavé, že u modelovaného odtoku dochází k podstatnému snížení zbytkové chyby pro prezentované charakteristiky ve všech časových měřítcích.

Obr. 3 a 4 ukazují míru korelace mezi veličinami přes různá časová měřítka ve čtyřech sezonách. Lze pozorovat, že korelace pro odtok a srážku je pozitivní, naopak pro teplotu a srážku a odtok a teplotu je korelace spíše negativní. Ve všech případech míra korelace roste s časovým měřítkem. Dále je vidět, že základní průběh korelace mezi sledovanými veličinami zůstává zachován pro simulovaná i korigovaná data a použití metody korekce systematických chyb má malý vliv na korelační strukturu. Nicméně dochází ke zlepšení v případě použití kaskádové korekce, zejména u korelace mezi srážkou a odtokem, kde lze pozorovat těsnější vztah mezi korigovanými a pozorovanými daty.

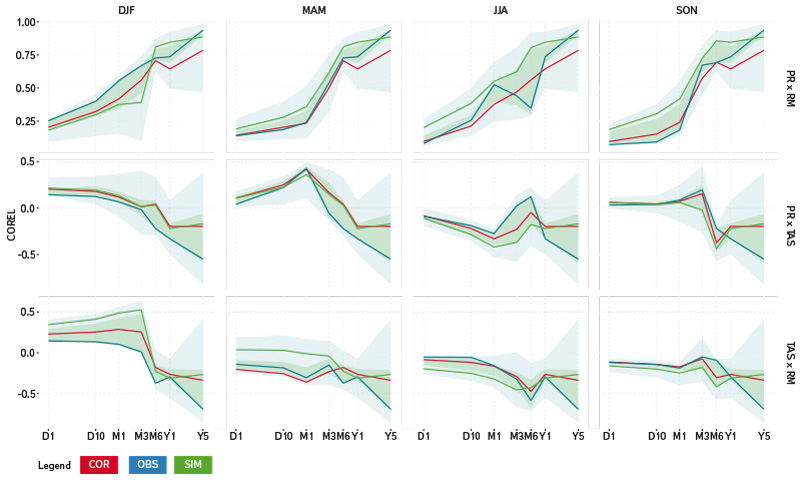
Obr. 4. Korelace mezi srážkou a modelovaným odtokem (nahoře), mezi srážkou a teplotou (uprostřed) a mezi teplotou a modelovaným odtokem (dole) pro jednotlivá roční období (DJF – zima, MAM – jaro, JJA – léto, SON – podzim); červeně jsou zobrazena korigovaná data kaskádovou kvantilovou metodou, modře pozorovaná data a zeleně simulovaná data; vodorovná osa značí časová měřítka (D1 – den, D10 – deset dnů, M1 – měsíc, M3 – tři měsíce, M6 – šest měsíců, Y1 – rok, Y5 – pět let); čáry značí průměrnou korelaci, zelený pás rozpětí 50 % a modrý pás 90 % ze všech modelů
Fig. 4. Correlation between precipitation and modelled runoff (above), between precipitation and temperature (middle) and between temperature and modelled runoff (below) for seasons of year (DJF – winter, MAM – spring, JJA – summer, SON – autumn); data corrected by the cascade quantile method are in red, observed in blue and simulated in green; horizontal axis shows time aggregation (D1 – a day, D10 – ten days, M1 – a month, M3 – three months, M6 – six months, Y1 – a year, Y5 – five years); the lines represent mean correlation coefficient, green (blue) area indicates an envelope of 50 (90)% of climate model simulations

Diskuse a závěr

Z prezentovaných výsledků je zřejmé, že korekce srážek a teploty pomocí standardní kvantilové metody není vhodná pro rutinní využití v hydrologických simulacích, jelikož v některých ročních obdobích vede ke značné zbytkové chybě modelovaného odtoku ve všech časových měřítcích kratších než rok, včetně denních hodnot, na kterých byla korekce kalibrována. Podobné výsledky prezentuje i Teng aj. [16]. Relativně největší zbytkové chyby se vyskytují v období nízkých průtoků (a v absolutním vyjádření se zpravidla jedná o nízké hodnoty).

Další výsledky (které nejsou kvůli rozsahu zahrnuty v tomto článku) ukazují, že podobné výsledky lze očekávat i u jiných povodí a při použití jiných hydrologických modelů. Východiskem může být využití nejnovějších (poměrně komplexních) metod popsaných Mehrotrou a Sharmou [17], které umožňují korigovat rozdělení pravděpodobnosti a korelační a autokorelační strukturu pro veličiny v různých časových měřítcích.

Úspěšnost těchto metod při hydrologických simulacích není nicméně zatím známa. Druhou možností je využití kombinací jednoduchých metod (např. přírůstková metoda, popř. aplikovaná v různých časových měřítcích) v kombinaci se stochastickými metodami umožňujícími generování dlouhodobé variability [18].

Poděkování

Tento článek vznikl v rámci řešení projektu „Možnosti kompenzace negativních dopadů klimatické změny na zásobování vodou a ekosystémy využitím lokalit vhodných pro akumulaci povrchových vod“ (TA04020501), který je spolufinancován Technologickou agenturou České republiky, a projektu „Půdní a hydrologické sucho v měnícím se klimatu“ (1616549S) financovaném Grantovou agenturou České republiky.